The exponential function is a type of mathematical function that can be used to a wide variety of problems that occur in the real world. Finding the exponential decay or increase, computing investments, modelling populations, and a variety of other applications are the primary uses for this tool.
Exponential functions:
An exponential function is a mathematical function that takes the form f (x) = ax. In this form, “x” represents a variable, and “a” represents a constant that is referred to as the base of the function. The base of the function must be greater than 0 in order for the function to be valid. The transcendental number e serves as the base of the exponential function more frequently than any other number, and its value is roughly equivalent to 2.71828.
Exponential function formula:
The formula f(x) = ax is the definition of an exponential function. In this formula, the input variable x appears in the form of an exponent. The exponential curve is dependent not only on the exponential function but also on the value that is used for x.
One of the most important mathematical functions is known as the exponential function, and it takes the form
f(x) = ax
Where a>0 and a is not equal to 1.
x is any real number.
If the variable is negative, the function is undefined for -1 < x < 1.
Here,
“x” is a variable
“a” is a constant, which is the base of the function.
The exponential function determines whether the growth or decay of an exponential curve occurs. Any number that either increases or decreases over time by a predetermined percentage at set intervals must exhibit either exponential growth or exponential decay.
Exponential growth:
Exponential Growth is characterised by a beginning phase in which the quantity grows very slowly, followed by a phase in which it grows very quickly. Over the course of time, the rate of change quickens. The passage of time results in a quickening of the rate of expansion. The term “exponential increase” describes the rapid expansion that has been observed. The following formula can be used to define exponential growth:
y = a ( 1+ r )x
Where r is the growth percentage.
Exponential decay:
In the process known as Exponential Decay, the quantity initially falls very quickly and then gradually. The rate of change slows down throughout the course of time. As more time passes, the rate of change will eventually slow down. The quick rise was supposed to represent a “exponential drop.” The following formula can be used to define exponential growth:
y = a ( 1- r )x
Where r is the decay percentage.
Exponential function derivative:
Let’s move on to the next topic, which is the derivative of exponential functions.
The value of ex is the same as its derivative with respect to x, written as d(ex)/dx = ex.
It is important to note that the exponential function, denoted by f(x) = ex, possesses a unique quality. It indicates that the value of the function’s derivative is the same as the value of the function itself.
f ‘(x) = ex = f(x)
Exponential function properties:
The qualities of an exponential function are represented graphically by the exponential graph of a function.
Consider the exponential function, which is written as y = 2x.
The graph of the function y = 2x can be seen in the following illustration.
Graph of the Exponential Function with the Equation y = 2x
The following describes the characteristics of the graph of the exponential function when the base is bigger than 1.
The point is traversed by the graph at this position (0,1).
All real numbers are contained inside this domain.
The parameters are y > 0
The line on the graph is climbing.
As x approaches negative infinity, the graph starts to behave asymptotically with respect to the x-axis.
As x gets closer to positive infinity, the graph continues to expand without limit.
The line on the graph is uninterrupted.
The line chart is unbroken.
The graph of the function y = 2-x is displayed up there for your perusal. When the base value is between 0 and 1, the following describes the features of the exponential function as well as its graph.
The line goes right through the middle of the point (0,1)
The range encompasses all numbers that are real.
The range is from y greater than 0
It creates a downward trend on the graph.
As x approaches a positive infinity, the line in the graph that can be seen above becomes asymptotic to the x-axis.
As x gets closer to negative infinity, the line continues to increase without limit.
It is a graph that is continuous.
It creates a nice looking graph.
Exponential function graph:
The graph of x’s exponents is shown in the following figure for your reference. As the value of the exponent goes up, it is possible to observe that the curves get more steep, and the rate of growth also goes up in proportion. Therefore, if x is more than one, the value of y = fn(x) will go up as the value of x goes up (n).
As can be observed from the discussion that has taken place thus far, the characteristics of polynomial functions change depending on the degrees they contain. The rate of growth of any polynomial function is proportional to the degree of the function. If an is more than one, then the function y = f(x) = ax is considered to have a more rapid rate of increase than polynomial functions. It follows that the growth rate of the function f (x) is stated to be greater than that of fn for any of the positive integers n. (x).
Therefore, the definition of the exponential function y = f(x) = ax for bases bigger than one is as follows: y = f(x) = ax. The set of all real numbers that are positive is referred to as the range, while the set that contains all real numbers that are negative is known as the domain of the exponential function.
Conclusion:
When analysing the growth or decline of a market, using exponential functions is critical in economics. Examples of models include the value of an investment that grows by the same % every period, sales of a company that grow by the same percentage every period, models of economic growth, and models of the spread of an epidemic.
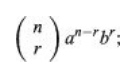
The index r takes on the values 0, 1, 2,…, n in the succession of phrases. The formula defines the coefficients, often known as binomial coefficients.
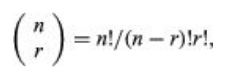
Here n! (also known as the n factorial) is the product of the first n natural integers 1, 2, 3,…, n (where 0! is equal to 1). The coefficients can also be found in what is known as Pascal’s triangle, an array.
The theorem may be used to find permutations, combinations, and probabilities in algebra. Islamic and Chinese mathematicians of the late mediaeval period were aware of the theory for positive integer exponents, n.
Properties of Binomial Expansion
- There are n+1 words in all.
- The first phrase is xn, while the last word is yn.
- As we move from the first to the last phrase, the exponent of x decreases by one. The exponent of y increases by one, whereas the exponent of x increases by one. Furthermore, the sum of both exponents in each phrase equals n.
- By multiplying the coefficient of each part by the exponent of x in that word and dividing the product by the number of that term, we can find the coefficient of the following phrase.
Properties of Binomial Theorem
- Every binomial expansion has one more term than the power of the binomial.
- When the exponents of each term in the expansion are totalled, the result is a sum equal to the binomial power.
- With each subsequent term in the expansion, the powers of the first term in the binomial fall by one, while the powers of the second term grow by one.
- It’s worth noting that the coefficients are symmetrical.
Binomial Theorem for Negative Index

When applying the binomial theorem to negative integers, we first set the upper limit of the sum to infinity; the sum will then only converge under specific conditions. Second, we use complex values of n to extend the definition of the binomial coefficient.
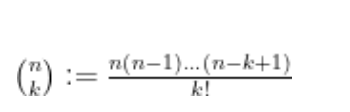
If x is a complex number, then xk is defined for every non-negative integer k — we just multiply twice and define x0 = 1 (even if x = 0). However, unless the value is a positive real, defining a non-integer power of a complex number is difficult.
Conclusion
Now that we have proved the binomial theorem for negative index n, we may deduce that:
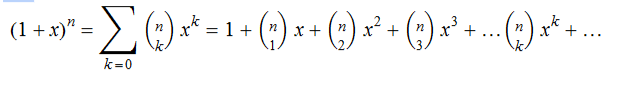
When the condition is true for any integral n, then when n is negative, |x|1
To answer basic mathematics issues, Newton devised the binomial series. Since the binomial series is such a basic mathematical tool, it’s important to have a strong understanding of it so you can utilise it in a variety of scenarios. The above guide is an easy way for you to understand binomial theorem and binomial theorem for negative indexes.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






