Profile
Settings
Refer your friends
Sign out
Various components of nature display the trait of continuity. The rivers have a constant flow of water. Human life is a continual flow of time, which means you are constantly becoming older. And so forth. Similarly, in mathematics, we have the concept of function continuity.
Simply put, a function is considered to be continuous if its curve can be sketched on a graph without raising your pen even once (provided that you can draw well). It’s actually a very simple and near to correct definition. However, we must define it more precisely for the sake of higher mathematics. That is exactly what we will do in this part. So let’s get started!
Definition
If the following three conditions are met, a function f(x) is said to be continuous at the point x = a in its domain:
f(a) exists (that is, its value is finite).
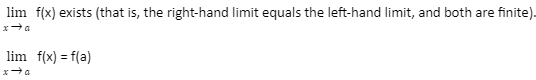
If the three conditions listed above are met for every point in the interval I, the function f(x) is said to be continuous in the interval I = [x₁,x₂].
However, we do not need to consider both the right-hand and left-hand limits for the computation of Limx→a f at the end-points of the interval I. (x). Only the right-hand limit must be considered for a = x1, and only the left-hand limit must be considered for a = x2.
Types of Continuity
- In certain periodic intervals, trigonometric functions (sin x, cos x, tan x etc.)
- (x² +x +1, x⁴ + 2, etc.) Polynomial Functions.
- Functions of Exponentials (e2x, 5ex etc.)
- In their domain, logarithmic functions (log 10 x, ln x² etc.)
The Function Is Expressed at x = a
When x=a, a function f(x) is said to be continuous.
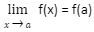
If a function is continuous at each point in the interval [a,b], it is said to be continuous on that interval.
This definition also implicitly assumes the existence of both f(a) andxa f(x) = f(a). If either of these are missing, the function at x=a will not be continuous.
The following fact can be derived from this definition.
When x=a, f(x) is continuous.
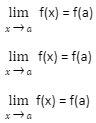
With the exception that we have changed the phrase “fine enough” with continuous, this is the identical information that we first jotted down when we first started looking at limits.
It’s great to finally understand what we mean when we say “good enough,” but the definition doesn’t fully explain what it means for a function to be continuous. Let’s look at an example to better grasp what it means to have a continuous function.
The Limit of the Function as the Approaching of X Takes Place, a Exists
The value of a function when x=a is equal to the function’s limit as x approaches a.
Only if the function in question is continuous at x=a is the preceding assertion true. Assume that at the specified location, some function f is continuous. Symbolically,
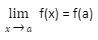
The following is an explanation of what it implies.
Consider the function f. a Select a fixed point (constant). (Again, the function must be continuous at all times.) At this point, evaluate the function to get f(a).
Now evaluate the function at various x-points around a. To put it another way, evaluate it at places that are slightly less than and slightly bigger than a, but not exactly equal to a. (‘Slightly less than’ and ’slightly greater than’ are used to signify ‘arbitrarily close to’ in this context.)
You’ll notice that the closer your point x comes to a, the closer the function value f(x) at those locations gets to f(a). That is what the term “limit” refers to.
The statement in the question is, by the way, employed in the definition of function continuity.
Conclusion
The phrase “continuous” is just a mathematical term. It’s not a technique, a method, an algorithm, or a theory. It’s simply a term for a specific type of function. As a result, it can’t be “applied” any more than the word “blue” can. Because the Mean Value Theorem is a genuine theorem, you may have said “what are real-life applications of the Mean Value Theorem.” Theorems and methods can be used, but language and meanings cannot.
If a function has a derivative, it is continuous; consequently, every differentiation problem is based on continuity. Differential equations can be used to describe everything from ocean tides to market prices, and you can’t solve any DE without continuous functions.
However, certain models are not continuous: for example, if a call centre is counting the number of phone calls they receive each minute, this is an integer-valued function that would not be continuous. All you’d have is a grid of dots. However, using a continuous function, one can “interpolate” the data (i.e. connect the dots) and then apply calculus methods.
