Inequality can be seen from a variety of perspectives, all of which are linked. The most prevalent indicator is Income Inequality, which measures how equally income is distributed across a population. Lifetime Disparity (income inequality over a person’s lifetime), Inequality of Wealth (distribution of wealth among households or individuals at a specific point in time), and Inequality of Opportunity are all related concepts (impact on the income of circumstances over which individuals have no control, such as family socioeconomic status, gender, or ethnic background). All of these inequality concepts are interconnected and provide various but complementary insights into the causes and consequences of inequality, thereby assisting governments in developing appropriate policies to combat inequality.
Definition
Inequality is a relation in mathematics that compares two numbers or other mathematical expressions in an unequal. It’s most commonly used to compare two numbers on a number line based on their size. Different types of inequalities are represented using a variety of notations:
- The symbol a b indicates that an is less than b.
- The symbol a > b denotes that an is larger than b.
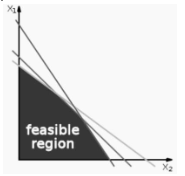
A set of inequalities defines the viable regions of linear programming.
A is not equivalent to b in any scenario. Strict inequalities are relationships in which an is strictly less than or strictly greater than b. Equivalence is not considered.
There are two forms of inequality relations that are not strict, in contrast to strict inequalities:
- The symbols a b or a b indicate that an is less than or equal to b. (Alternatively, at most b, or not more than b)
- The symbols a b or a b indicate that an is greater than or equal to b.(Or, to put it another way, at least b, or not less than b).
A b, the symbol for “greater than” bisected by a slash, “not,” can also be used to express the connection not greater than. Not less than and a b are in the same boat.
The symbol a b denotes that an is not equal to b; this inequation is frequently referred to as a sort of rigorous inequality. It makes no claim that one is superior to the other, nor does it require that a and b belong to an ordered set.
Triangle Inequality Theorem
According to the triangle inequality theorem, the total of two sides of a triangle is always greater than the third side. The Triangle is a polygon defined by three line segments. It is the smallest polygon conceivable. Three sides, three vertices, and three internal angles make up a triangle. Triangles are classified according to their angle measurement and side length. The inequality theorem applies to all triangles, including equilateral, isosceles, and scalene triangles. Let’s take a closer look at this theorem and its proof.
Triangle Inequality Theorem Proof
The relationship between the three sides of a triangle is described by the triangle inequality theorem. The total of the lengths of two sides of any triangle is always bigger than the third side, according to this theorem. In other words, the shortest distance between two unique points is always a straight line, according to this theorem.
Consider the ∆ABC diagram below, with the side lengths a, b, and c.
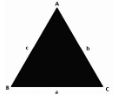
According to the triangle inequality theorem,
a < b + c,
b < a + c,
c < a + b
The Perpendicular is the smallest distance between any vertex and the opposite side of any triangle. XP is the shortest line segment from vertex X to side YZ in the diagram below.
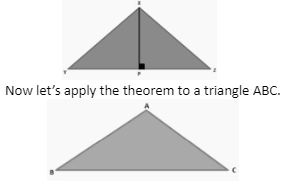
To Prove: |BC|< |AB| + |AC|
Consider an ∆ABC structure. Extend the side AC to a point D, as illustrated in the diagram below, so that AD = AB.
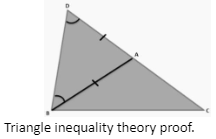
Triangle inequality theory proof.
Reverse Triangle Inequality
The reverse triangle inequality is a simple result of the triangle inequality that offers lower bounds rather than higher bounds. The statement for flat geometry is:
Any of the triangle’s sides are more than or equal to the difference between the other two.
The statement in the case of a normed vector space is:
|||x|| – ||y||| ≤ ||x-y||
Or for metric spaces,
|d(y, x) – d(x, z)| ≤ d(y, z). This implies that the norm ||·||, as well as the distance function d(x,·), are Lipschitz continuous with Lipschitz constant 1, and therefore are in particular uniformly continuous.
Generalized Triangle Inequality
The triangle inequality asserts that the sum of the lengths of any two sides of a triangle must be larger than or equal to the length of the remaining side in mathematics. This assertion allows degenerate triangles to be included, although some authors, particularly those writing about introductory geometry, will rule out this possibility, leaving equality out. If the lengths of the triangle’s sides are x, y, and z, and no side is longer than z, the triangle inequality asserts that
z ≤ x + y,
Only in the degenerate case of a triangle with zero area does equality exist. The triangle inequality is a distance theorem formulated using vectors and vector lengths (norms) in Euclidean geometry and some other geometries:
||x+y|| =||x|| + ||y||
Where the third side’s length z has been substituted by the vector sum x + y When x and y are real numbers, they can be seen as vectors in R¹ and the triangle inequality expresses an absolute value relationship.
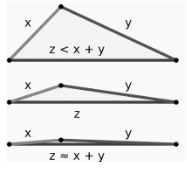
The triangle inequality is a corollary of the Pythagorean theorem for right triangles and the law of cosines for generic triangles in Euclidean geometry, though it can be proved without these theorems. In R² or R³, inequality can be readily seen. Three examples are shown to the right, starting with apparent inequality (top) and progressing to equality (bottom) (bottom). In the Euclidean instance, equality is only achieved if the triangle contains a 180° angle and two 0° angles, resulting in the three vertices being collinear, as shown in the bottom example. In Euclidean geometry, the shortest distance between two points is thus a straight line.
Conclusion
When determining the optimum solution to a problem, a system of linear inequalities is frequently used. This answer could be as straightforward as estimating how many units of a product should be manufactured in order to maximise profit, or as complex as determining the best medicine combination to give a patient.
We’ll use a strategy similar to the one we used to answer applications with equations to solve applications with linear inequalities. We’ll go over the situation and make sure we understand everything. Then we’ll figure out what we’re looking for and assign a variable to it. To make it easier to translate into an inequality, we’ll restate the problem in one statement. The inequality will then be resolved.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






