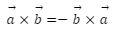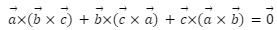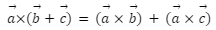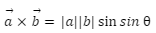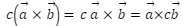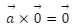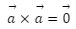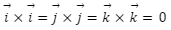A Short Note on Cross Product Properties
In this article we will cover Cross Product Properties, Anti-commutative property, Jacobi property, distributive property. The cross-product properties are useful for clearly understanding vector multiplication and for quickly solving all vector calculation problems. The properties of the cross product of two vectors are as follows: It has anti-commutative, Jacobi, and distributive properties. When two parallel vectors are cross-product, the result is zero. The cross product of two vectors equals the area of a parallelogram formed by them.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out