Profile
Settings
Refer your friends
Sign out
The addition rule for non-mutually exclusive events is applicable when two outcomes are possible and the occurrence of one does not preclude the occurrence of the other.
This scenario differs from the one depicted in the preceding section due to the probability of overlap, P(A and B), which is supplied. Since the addition rule is used to determine the likelihood that either one or the other event will occur, the likelihood that both events will occur concurrently must be deducted from the outcome.
Probability and Addition Theorem
In probability, addition concepts are crucial. If we are aware of the probabilities of events “A” and “B,” we can use these criteria to determine the likelihood of either happening. The set theory symbol U, which represents the union of two sets, can occasionally be used in place of the word “or.” Whether or not events A and B are mutually exclusive determines which addition rule should be applied.
The probabilities of the two events are simply added together in the first formula. The probability that both occurrences will occur is subtracted from the sum of the probabilities of the two events in the second formula.
If two events A and B are exclusive of one another, then
Theorem: P(A B)=P(A)+P(B)-P(A∩B)
Where,
P(A ∪B) = Probability that A or B will occur
P(A)= The probability of Event A
P(B) = The probability of Event B
Proof:
Consider the
n=total number of exhaustive cases
n1=no. of cases favorable to A
n2=no. of cases favorable to B
We currently have two events—A and B—that cannot both occur. Therefore n1+n2 is the number of A or B-favorable cases.
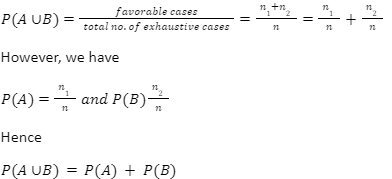
Mutual Exclusivity
A statistical phrase for two or more events that cannot coincide is “mutually exclusive.” It is frequently used to refer to circumstances in which the occurrence of one event takes precedence over the other. Take rolling the dice as a simple illustration. On the same die, you cannot simultaneously roll a three and a five. Additionally, getting a three on the first roll has no bearing on whether a later roll results in a five or not. Every die roll is a distinct occasion.
Addition Rule for Independent Events
When it comes to probability, two occurrences are deemed independent if the occurrence of one has no bearing on the likelihood that the other will happen. Dependent occurrences, on the other hand, are those whose probabilities influence one another.
Example of Addition Theorem
Example
What is the probability that an issue will be solved if two students, Paul and Jimmy, each have a 50% and a 33% chance of doing so?
Solution
Let A and B represent the chances of Paul and Jimmy solving the issue, respectively.Then ,
If the issue is resolved by at least one of them as well, the issue will be resolved.
So, we must locate P(AUB)
Using the probability addition theorem, we have
P(AUB) = P(A) + P(B)- P(A∩B)
What is the use of the addition theorem in probability?
One must add the odds of each occurrence occurring in the case of mutually excusable events. The probabilities of each event occurring separately must be added, and the probability of the events occurring simultaneously must be subtracted, in the case of non-mutually exclusive events.
The probability that at least one of the events occurs is calculated using the addition rule for probabilities. The area of mathematics known as probability is the study of how certain or uncertain an event or series of events is.
Conclusion
In this article, the scenarios in which the probability of a union of events can be determined by adding probabilities together are given by the probability rule of addition. It is frequently used when two occurrences are mutually exclusive, or when they cannot occur simultaneously.
The probability that at least one of the events occurs is determined using the probabilities addition rule. It is possible to define probability as the area of mathematics that measures how certain or uncertain an event or series of events is.
