A General Overview of De Morgan’s Laws

The intersection and union of sets can be related through complements thanks to De Morgan’s Law, which is a pair of transformation rules in boolean algebra. These rules are used to relate the two concepts. In accordance with De Morgan’s Law, there are two prerequisites that must be satisfied. The primary function of these conditions is to condense expressions into a more understandable format. Calculations and the resolution of difficult boolean expressions are made simpler as a result of this improvement.

The complement of the union of two sets will, in accordance with De Morgan’s Law, be equal to the complement of the intersection of the complements of each set individually. In addition to this, the complement of the intersection of two sets will be the same as the union of the complements of the sets individually. Using Venn diagrams, one can quickly get a visual representation of these laws. In this article, we are going to go through the claims of De Morgan’s Law, as well as the verification of these statements, some applications of the law, and some examples of it in action.

De Morgan’s Laws: An overview

In the field of set theory, Demorgan’s laws are a collection of two postulates that are utilised quite frequently. The term “set” refers to a collection of well-defined and unique objects that come together to create a group when they are gathered together. De Morgan’s laws are what we turn to when we want to simplify operations involving sets, such as finding the complement, the union, and the intersection of sets.

De Morgan’s Law Statement

Both boolean algebra and set theory can benefit from the use of Demorgan’s law, which serves to simplify mathematical equations. Let us suppose that we have a universal set U, and that there exist two sets A and B that are subsets of U. The complement of set A is denoted by the superscript A’ whereas set B complement is denoted by B’. The symbol for the union is the letter ‘U’ while the symbol for the intersection is the letter ‘∩’.

De Morgan’s Law of Union

The complement of the union of the two sets A and B will be equal to the intersection of A’ (the complement of A) and B’, according to the Law of Union proposed by De Morgan (complement of B). Another name for this concept is “De Morgan’s Law of Union.” It is express mathematically as (A ∪ B)’ = A’ ∩ B’.

De Morgan’s Law of Intersection

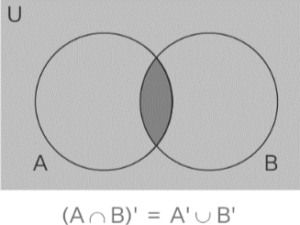
According to the law of intersection that was developed by De Morgan, the complement of the intersection of A and B will be equal to the union of A’ and B’. This particular circumstance is referred to be De Morgan’s law of Intersection. It is possible to derive it by writing (A ∩ B)’ = A’ ∪ B’.

Conclusion

Both basic algebra and Boolean algebra make use of De Morgan’s law in their respective curriculums. This law, which helps to reduce difficult expressions, is frequently used in most engineering industries to design hardware and simplify procedures. This is because the law helps to reduce the number of variables involved. Several further uses of De Morgan’s law are discussed in the following sections.

Applications of De Morgan’s law can be observed in electronic engineering, namely in the development of logic gates. Equations conforming to this law can be derived by employing only the NAND (AND negated) or NOR (OR negated) gates as the only logical building blocks. Because of this, the cost of the hardware is reduced. Additionally, NAND, NOT, and NOR gates are simpler to build in practise than AND gates.

In computer programming, Demorgan’s law is a fundamental concept. This law contributes to the simplification of logical expressions that are written in codes, which ultimately results in a reduction in the number of lines. As a result, it contributes to the code’s overall efficiency and effectiveness. In addition, the verification process for SAS codes is greatly simplified and speed up as a result of these laws.