A Detailed Thread about Trigonometric Ratios

The trigonometric ratios are sine, cosine, tangent, cotangent, cosecant, and secant. A subfield of geometry known as trigonometry, trigonometry is a branch of mathematics that deals with the sides and angles of triangles with right angles. Therefore, trigonometric ratios are evaluated in relation to the sides and angles of the triangle.

The values of all the trigonometric functions are based on the value of the ratio of sides in a right-angled triangle. Trigonometric ratios are defined as the values of all of these ratios. The trigonometric ratios of a certain angle are determined by comparing the lengths of the sides of a right-angled triangle to each other in relation to one of the triangle’s acute angles.

The following are the three sides that make up a right triangle:

• Hypotenuse (the longest side)
• Perpendicular (opposite side to the angle)
• Base (Adjacent side to the angle)

How to Find Trigonometric Ratios?

Take into consideration a triangle that has a right angle at point B.

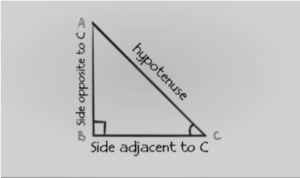
In relation to ∠C, the following is a table including the trigonometric ratios:

• sine:The ratio of the side that is opposite (perpendicular side) to an angle to the hypotenuse is what is meant when we talk about the sine of that angle.
• cosine:The cosine of an angle is calculated by dividing the side that is adjacent to the angle by the hypotenuse.
• tangent:The ratio of the side that is perpendicular to an angle to the side that is next to that angle is the definition of the tangent of that angle.
• cosecant:The cosecant is an example of a multiplicative inverse of the sine function.
• secant:The multiplicative inverse of cosine is denoted by the symbol secant.
• cotangent:The multiplicative inverse of the tangent is denoted by the term “cotangent.”

The ratios that have been discussed thus far can be shortened as sin, cos, tan, cosec, sec, and tan, respectively, in the order that they are presented. The following are the ratios that are defined for ABC:

• sin C = (Side opposite to ∠C)/(Hypotenuse) = AB/AC
• cos C = (Side adjacent to ∠C)/(Hypotenuse) = BC/AC
• tan C = (Side opposite to ∠C)/(Side adjacent to ∠C) = AB/BC = sin ∠C/cos ∠C
• cosec C= 1/sin C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/AB
• sec C = 1/cos C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/BC
• cot C = 1/tan C = (Side adjacent to ∠C)/(Side opposite to ∠C)= BC/AB

If we assume that angle ∠A is 30 degrees and angle ∠C is 60 degrees in a right triangle ABC, then there can be an unlimited number of right triangles with those specifications; yet, the ratios mentioned above for angle ∠C will remain the same in all of those triangles. Therefore, every right triangle will have the same ratios for any of the acute angles (whether ∠A or ∠C). This indicates that the ratios do not depend on the lengths of the sides that make up the triangle.

Trigonometric Ratios Table

The following table provides the trigonometric ratios for a few specific angles, including 0 °, 30 °, 45 °, 60 ° and 90° . These ratios are frequently employed in mathematical calculations.

From this table, we can find the value for the trigonometric ratios for these angles. Examples are:

Sin 30° = ½

Cos 90° = 0

Tan 45° = 1 

Trigonometric Ratios of Complementary Angles Identities

Complementary angles are a pair of angles that, when added together, equal a whole number that is exactly 90 degrees. (90° – θ) is the complement of an angle. The following are the trigonometric ratios that apply to complementary angles:

• sin (90°- θ) = cos θ
• cos (90°- θ) = sin θ
• cosec (90°- θ) = sec θ
• sec (90°- θ) = cosec θ
• tan (90°- θ) = cot θ
• cot (90°- θ) = tan θ

Pythagorean Trigonometric Ratios Identities

The Pythagorean theorem is the starting point for deriving the identities of the trigonometric ratios that use the Pythagorean system. The following is what we obtain when we apply the Pythagorean theorem to the triangle with a right angle:

Opposite2 + Adjacent2 = Hypotenuse2

Dividing both sides by Hypotenuse2

Opposite2/Hypotenuse2 + Adjacent2/Hypotenuse2 = Hypotenuse2/Hypotenuse2

• sin2θ + cos2θ = 1

This is one of the important Pythagorean identities. In the same way, we can derive two other Pythagorean trigonometric ratios identities:

• sin2θ + cos2θ = 1
• 1 + tan2θ = sec2θ
• 1 + cot2θ = cosec2θ

Sum, Difference, Product Trigonometric Ratios Identities

The identities of the trigonometric ratios for sum, difference, and product contain the formulas for sin(A+B), sin(A-B), cos(A+B), and cos(A-B), amongst others.

• sin (A + B) = sin A cos B + cos A sin B
• sin (A – B) = sin A cos B – cos A sin B
• cos (A + B) = cos A cos B – sin A sin B
• cos (A – B) = cos A cos B + sin A sin B
• tan (A + B) = (tan A + tan B)/ (1 – tan A tan B)
• tan (A – B) = (tan A – tan B)/ (1 + tan A tan B)
• cot (A + B) = (cot A cot B – 1)/(cot B – cot A)
• cot (A – B) = (cot A cot B + 1)/(cot B – cot A)
• 2 sin A⋅cos B = sin(A + B) + sin(A – B)
• 2 cos A⋅cos B = cos(A + B) + cos(A – B)
• 2 sin A⋅sin B = cos(A – B) – cos(A + B)

Conclusion

Mathematically speaking, trigonometry is the study of the relationships between the lengths of the sides and the angles of right triangles (triangles with one angle that is exactly 90 degrees). When referring to an angle, the terms opposite and adjacent are used to describe the locations of the three sides that make up any triangle. There are an extremely large number of situations in which trigonometry and its functions can be useful. For example, it is used in geography to measure the distance between different landmarks, in astronomy to estimate the distance between nearby stars, and in the satellite navigation system to calculate the distance between different satellites.