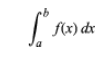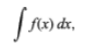A Brief Note on Types of Integrals

Integral, in mathematics, a numerical value equal to the area below the graph of a function at a given interval (determined integral), or a new function whose derivative is the original function (indefinite integral). These two meanings relate to the fact that definite integrals of any integrable function can be found using indefinite integrals and results from the fundamental theorem of calculus. The definite integral of the function f (x) (also known as the Riemann integral) is expressed as:

(See Integral [About Symbols]) And equal to the area of ​​the area surrounded by the curve (if the function between x = a and x = b is positive) y = f (x), x-axis and row x = a and x = b. Indefinite integral of the function f (x) (sometimes called indefinite integral).

A function whose derivative is f (x). The indefinite integral is not unique because the derivative of the constant is zero. The process of finding an indefinite integral is called an integral.

Integration:

 In differentiation, we have studied to get a set of families of functions in an interval if the function f is differentiable within an interval, for example I. If the value of the function is known within the interval, is there a way to know about the function? 

 This process is the opposite of finding the derivative. Integration is primitive. Integration is a way to add parts to find the whole thing. Integration is the whole pizza, and fragments are a differentiating feature that can be integrated. If f (x) is an arbitrary function and f'(x) is its derivative. The integral of f'(x) to dx is given as 

 ∫ f'(x) dx = f (x) + C.

Types of integration: 

There are two forms of integration. 

• Indefinite integral: If there is no limit to the integral, it is the integral of the function. Contains any constant. 
• Definite integral: Integral of a function with integral limits. There are two values ​​for limiting the integration interval. One is the lower limit and the other is the upper limit. It does not include constants of integration.

Constant of integration:

 The constant of integration represents a sense of ambiguity. For a given derivative, there can be many integrals that can vary depending on the set of real numbers. This set of real numbers is represented by the constant C.

Antiderivative:

 In the calculation, the indefinite integral, inverse function, primitive function, primitive integral, or indefinite integral [Note 1] of the function f is a divisible function F whose derivative is equal to the original function f. This can be given symbolically as F` = f. The process of solving an indefinite integral is called the inverse derivative (or indefinite integral), and the opposite operation is called the derivative, which is the process of finding the derivative. Indefinite integrals are often represented by uppercase Roman numerals such as F and G. 

 The indefinite integral is associated with the definite integral by the second law of analysis: the definite integral of a function in a closed interval where the function is Lehman integrable is equal to the difference between the values ​​of the indefinite integral evaluated at the endpoints. Will be the interval.

Riemann integral:

 In the field of mathematics known as real analysis, the Riemann integral created by Bernhard Riemann was the first rigorous definition of the integral of a function on an interval. It was submitted to the Faculty of the University of Göttingen in 1854, but was not published in the journal until 1868. In many functions and practical applications, Riemann integrals can be evaluated by the fundamental theorem of calculus or approximated by numerical integration.

Roughly speaking, the Riemann integral becomes the limit of the Riemann sum of the function as the partition becomes finer. If there is a limit, the function is said to be integrable (more accurately, Riemann integrable). The Riemann sum can be arbitrarily approximated to the Riemann integral by making the partition sufficiently fine.

Lebesgue integration:

 In mathematics, the integral of a non-negative function of a single variable can be seen most simply as the region between the graph of that function and the x-axis. Named after the French mathematician Henri Lebesgue, the Lebesgue integral extends the integral to a larger class of functions. It also extends the domains in which these functions can be defined. 

 Long before the 20th century, mathematicians understood non-negative functions with sufficiently smooth graphs, such as polygons. However, if it becomes necessary to deal with more irregular functions-Example: B. A more careful approximation procedure to define a suitable integral as a result of the limiting process of theoretical analysis and mathematical probability theory. It became clear that was necessary. You may also want to integrate a space that is more general than a real line.  Lebesgue integration provides the necessary abstraction for this. 

 The Lebesgue integral plays an important role in many other areas of probability theory, real analysis, and mathematics. It is named after Henri Lebesgue (1875–1941), who introduced the integral (Lebesgue 1904). It is also a central part of axiomatic probability theory. 

 The term Lebesgue integral means either the general theory of integrals of functions for general measures introduced by Lebesgue, or the special case of integrals of functions defined by the solid subdomain of Lebesgue. It is an average measure.

CONCLUSION

However, Riemann integrals do not interact well with assuming the boundaries of a sequence of functions, making it difficult to analyse such constraint processes. This is important, for example, when studying Fourier series, Fourier transforms, and other topics. The Lebesgue integral can better explain how and when it can be bounded under the integral symbol (via the monotone convergence theorem and the dominant convergence theorem).