A Brief Analysis of Circles, Conic Sections

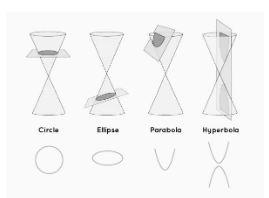
The curves formed by the intersection of a plane with a cone are known as conic sections or cone sections. A cone or conic section has three principal sections: parabola, hyperbola, and ellipse (the circle is a special kind of ellipse). The conic portions are made using a cone with two identical nappes.

Although the shapes of the sections of a cone or conic sections vary, they all share some common qualities, which we shall discuss in the following sections.

Conic Sections:-

Conic sections are the curves created by cutting a cone with a plane. Nappes are two similar conical shapes that make up a cone. Depending on the angle of the cut between the plane and the cone and its nappe, we can get a variety of shapes. We generate the following shapes by cutting a cone with a plane at various angles:

• Circle
• Parabola
• Ellipse
• Hyperbola

The above mentioned figure depicts the various conic sections and how they are formed from the cones.

Circle:-

The circle is a sort of ellipse in which the cutting plane is parallel to the cone’s base. The circle’s focus is known as the circle’s centre. The radius of the circle is the distance between the locus of the points on the circle and the focus or centre of the circle. For a circle, the value of eccentricity€ is e = 0. There is no directrix in Circle. The general version of the equation for a circle with a radius of r and a centre at (h, k):

                                                                 x-h2+ y-k2 = r2

A circle is a fundamental two-dimensional form whose radius is measured. The circles divide the aircraft into two areas: the interior and the exterior. It’s similar to the line segment type. Assume the line segment is bent around till the ends meet. Make sure the loop is perfectly circular.

The circle is a two-dimensional figure with a circumference and an area. The circumference, or distance around the circle, is also known as the circle’s perimeter. 

Properties of circle:-

Some of the most fundamental basic characteristics of circles are as follows:

• The outer line of a circle is equidistant from its centre

• The circle’s diameter divides the circle into two equal parts, known as semi-circles
• If any two circle are having same radius then they are said to be congruent circles
• The diameter, which is twice the radius, is the circle’s largest chord

Real life application:-

In real life, circles can be found in both natural and human things. Many domestic products have circles in their designs, such as cups, candles, and doorknobs.

In architecture, the circle plays a great role. It provides a good aesthetic look to the design with full of symmetry.

The wheel is still considered one of the most significant inventions of all time. People and things may travel longer distances at higher speeds thanks to this circle. Vehicle tyres, roundabouts on roadways, engine crankshafts, and road layout are all examples of circles in transportation. When calculating distance, GPS also uses circles.

All of the other characteristics can be determined if the circle’s radius is known. The parameters can be used to determine important information for real-world applications. Knowing the circumference of the planets, for example, allows us to compare their relative sizes, and artificial satellites put into orbits with specific circumferences.

Conclusion:-

A circle is a two-dimensional shape created by a set of points on the plane that are separated by a constant or fixed distance (radius). The centre of a circle is a fixed point in the plane and the radius is the fixed distance between that point and any point on the circle.

A circle is a planar shape formed by a closed curve with each point on the curve being the same distance from the circle’s centre. Everyone uses the concept of circles in geometry on a daily basis. It’s employed in education, agriculture and architecture.