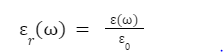Relative Permittivity of a Material

Relative permittivity is the property of a particular dielectric material that determines what static energy can be stored per unit volume of the dielectric material per unit voltage applied to it, and it’s of great importance for capacitors and capacitance calculations. Permittivity is denoted within equations using the symbol ε (epsilon). It measures the electric polarisability of a dielectric medium.

Usually, materials with high permittivity polarise higher in response to an applied electric field as compared to a material that offers low permittivity. Therefore, they can store more energy within the given material. Both permittivity and dielectric constant hold the same meaning for most of their given purposes, but there are instances where these terms do have different meanings.

Relative Permittivity

The age-old term for relative permittivity is also called dielectric constant. It is still often used, but lately, the standards of many organisations have deprecated it because of its ambiguity; even some earlier reports have been using it for the absolute permittivity ε. Permittivity is often preferred either as a static property but can also be described as a frequency-dependent property. Relative permittivity may be used to denote the real component ε’r when the value of relative permittivity is a complex number.

Relative permittivity is generally denoted as εr(ω).

r()= ()0,

where () denotes the material’s complex permittivity, and ε0 denotes the vacuum permittivity.

A relative permittivity is a dimensionless number that’s generally complex-valued; its real and imaginary parts are given by

r()=r,() –r,,()

The relative permittivity of a medium is also related to the electric susceptibility of the same medium, χe, as

εr(ω) = 1 + χe

Usually, anisotropic media (e.g., non-cubical crystals) has relative permittivity as a second rank tensor. Relative permittivity of a material with a frequency of 0 is often its static relative permittivity.

The relative static permittivity, εr, is usually used to measure the static electric field. In the beginning, the capacitance of a certain capacitor, C0, is measured by the vacuum between the capacitor plates. After this, using the same capacitor and the same distance between its plates, capacitance C is measured by placing a dielectric between the capacitor plates. The relative permittivity is calculated as

r= CC0.

The quantity mentioned above is converted into frequency-dependent for time-varying electromagnetic fields.

Applications of Relative Permittivity

The relative permittivity is a piece of information required to design capacitors and in various conditions and circumstances where the material is probably expected to induce capacitance into a circuit. Suppose a particular material with a high permittivity is placed in an electrical field. The value or magnitude of this field shall be brought down while within the volume of that particular dielectric. This fact is often used to raise the capacitance for a specific capacitor design. The layers beneath these etched conductors in the printed circuit boards and also over them act as dielectrics.

Using the relative permittivity of a solvent, one can approximate the chemical polarity of the solvent to a good extent. Water, for example, is a very polar solvent and the relative static permittivity of water at a temperature of 293 Kelvin is 80.10. Comparatively, the relative static permittivity of n-hexane, a non-polar solvent, at the same 293 Kelvin, is 1.89. This fact is used to create the different types of chromatographic techniques.

While relative permittivity gives a good measure to identify material through a chromatography test, the correlation must be treated with caution. An example of such an exception is dichloromethane and tetrahydrofuran. At 296 Kelvin, the relative static permittivity of dichloromethane is 9.08; it is highly insoluble in water. But in the case of tetrahydrofuran, the relative static permittivity at 295 Kelvin is 7.52. Accordingly, tetrahydrofuran should also be insoluble in water. However, tetrahydrofuran is highly soluble in water because the oxygen atoms in the molecules form hydrogen bonds with water molecules.

Relative permittivity can also be used to compare the polarisability of two entities. However, such correlation should be treated with caution. For example, the relative permittivity of acetic acid is 6.25, and that of iodoethane is 7.62. The iodine atom is easily polarisable; the relative permittivity of iodoethane should be less than that of acetic acid. However, that is not the case.

Importance of Relative Permittivity

Suppose a material with high relative permittivity is placed inside an electric field. Upon measuring the magnitude of the electric field inside the volume occupied by the dielectric, it can be observed that the electric field inside that volume is diminished. This property plays a vital role in creating a particular capacitor design with increased capacitance.

A larger relative permittivity is an indication that the material is more polarisable. A lower relative permittivity indicates that the material is not easily polarisable. In other words, a higher electric field is required to polarise the material.

Conclusion

The age-old term for relative permittivity is also called dielectric constant. It is still often used, but lately, the standards of many organisations have deprecated it because of its ambiguity; even some earlier reports have been using it for the absolute permittivity ε. Permittivity is often preferred either as a static property but can also be described as a frequency-dependent property. Relative permittivity may be used to denote the real component ε’r when the value of relative permittivity is a complex number.