Law of radioactive decay

What is Radioactive Decay?

Radioactive decay or radioactivity is the process in which an unstable nucleus decays or transforms into a stable nucleus by emitting particles. Radioactive decay was first discovered by Henry Becquerel in 1896. There are different types of radioactive decay based on the nature of the emitted particles. They are as follows:

(i) Alpha decay (α decay): In this type of decay, an alpha particle which is the Helium nucleus (He24 ) is emitted by the decaying nucleus.
(ii) Beta decay (β decay): In this type, beta particles (electrons or positrons) are emitted by the unstable nucleus. Positrons (e+) are particles that have the same mass as that of electrons but are positively charged unlike electrons. Based on whether the emitted particles are electrons or positrons the decay is termed as β–decay or β+decay.
(iii) Gamma decay (γ decay): In this type, the unstable nucleus decays by emitting high energy photons also called gamma rays.

Kinetics of Radioactive Decay

The kinetics of the radioactive decay is measured by the rate at which unstable nuclei disintegrate or decay into more stable nuclei.
Kinetics gives information about how many nuclei are present at any given instant of time.
It provides information about how long the unstable nuclei will continue to decay.

Law of Radioactive Decay

Let ‘N0’ be the initial number of nuclei of a radioactive sample present at time t=0 and ‘N’ be the number of nuclei at any time ‘t’. Then the rate of decay R is defined as the change in the number of nuclei per unit time. It is denoted by

Integrating both sides of the equation (3) gives,

Equation (5) is termed as the law of radioactive decay or the radioactive decay formula. Radioactivity follows the exponential decay law.

Radioactive Decay Formula:

The radioactive decay formula is given by equation (5). The formula indicates that the number of radioactive nuclei decreases exponentially with time. This is illustrated in the following figure. As time increases, the number of undecayed nuclei reduces in an exponential manner.

Unit of activity

The rate of decay (R) is also termed as the activity of the radioactive sample. The SI unit of activity is becquerel (Bq).

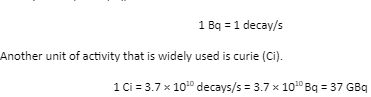
Different radioactive nuclei (also called radionuclides) have different decay rates or activities. There are two different quantities to measure the decay time of radionuclides. They are the half-life and the mean-life.

Half-life

It is the time taken for the number of nuclei (N) of a radioactive material to reduce to half of its initial value. It is denoted by T1/2.
Half-life is the time taken for N to decrease from its initial value N0 and reach N0/2.

Mean life

Another measure of the decay time of radionuclides is the mean life or average life denoted by τ.
Some nuclei in the radioactive sample have shorter decay time while other nuclei have longer decay times.
Mean life is the average of the decay times of all the nuclei in the sample.
It is determined by adding the decay time of all nuclei and dividing the sum by the total number of nuclei.

Applications:

Radioactivity is used in radiometric dating to find the ages of geological and biological specimens.
Radiocarbon dating, which makes use of decay of carbon atoms, is employed to determine the ages of Egyptian mummies, objects such as cloths, leathers, etc., from ancient civilizations.

Conclusion:

Radioactive decay is the decay of unstable nuclei into stable nuclei. The decay follows an exponential law given by the radioactive decay formula, N=N0e-torR=R0e-t. The SI unit of radioactivity is becquerel (Bq). Bq is related to another unit of radioactivity, namely,curie (Ci) as 1 Ci = 3.7 × 1010 Bq. The activity of a radionuclide is given by R =λN. The quantities used to measure the radioactivity are the half-life and mean life of the nuclei. Half-life is the time required for the number of radionuclides (N) or the activity (R) to reduce to half of its initial value. Mean life is the average time taken for the complete decay of the radioactive material. The half-life and mean life are related by equation (13).