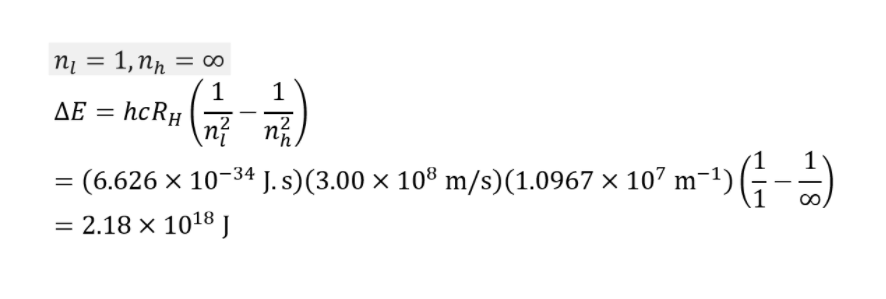Ionization Energy

Every element in the periodic table has Ionisation Energy, which can also be associated with the ionisation potential. So, what is ionisation energy? 

It is the energy required to remove an electron from an atom and generate an ion. Usually, we express it in kJ/mol, which is calculated on the basis of an isolated atom in its gaseous form. 

Let us look at how to calculate it. Then, we will discuss what the first and second ionisation energies mean and how it fluctuates over the periodic table.

We may use the following equation to calculate ionisation energy:

X + first Ionisation Energy → X+ + e–

where,

X is a neutral atom

X+ is an ion of atom X with a single positive charge

e– is an electron with a single negative charge

Expelling the first electron from an originally neutral atom takes less energy than removing the second, which requires less energy than dispelling the third, and so on. Each electron emitted needs the discharge of more energy. 

This aspect is because when the first electron is lost, the atom’s overall charge becomes positive, and the electron’s negative forces are attracted to the positive charge of the newly formed ion. The more electrons lost, the more positive this ion gets, making it more difficult to extract the electrons from the atom.

In principle, the further an electron is from the nucleus, the easier it is to evacuate. In other words, ionisation energy is related to atomic radius; the higher the radius, the less energy is told to eliminate the electron from the outer orbital. 

For example, removing electrons from Ca (Calcium) would be far easier than from Cl (Chlorine), where the electrons are closer to the nucleus.

Trends in Ionisation Energy Over Time

The energy required to extract electrons from gaseous atoms or ions is a chemical species’ ionisation energy (i.e., an atom or molecule). This property is known as the ionisation potential, which is measured in volts. In chemistry, it is commonly referred to as one mole of a substance (molar ionisation energy or enthalpy) measured in kJ/mol. 

In atomic physics, we often measure ionisation energy in electron volts (eV). The ionisation energy of large atoms and molecules is low, while the ionisation energies of microscopic molecules are higher.

The energy of ionisation of atoms in different atomic or molecular orbitals varies. The nth ionisation energy, in general, is the amount of energy required to remove the nth electron after the removal of the first n-1 electrons. 

We assume it as a measure of an atom’s or ion’s inclination to give an electron and the strength of the electron binding. The greater the ionisation energy, the more difficult it is to remove one electron. 

We can use an element’s ionisation energy to forecast its reactivity. Elements with low ionisation energy are reducing agents, creating cations that combine with anions to create salts.

Energies of Ionisation (First, Second, and Subsequent)

The amount of energy required to remove the outermost valence electron from a neutral atom is the initial ionisation energy. The second ionisation energy is the energy needed to remove the next electron, and so on. The second-ionisation energy is always larger than the first-ionisation energy.  

Consider an alkali metal atom. We can easily remove the first electron because its loss supplies the atom with a stable electron shell. When we remove the second electron, there is the formation of a new electron shell. This shell is closer and more tightly linked to the atomic nucleus.

We may use the following equation to represent the initial ionisation energy of Hydrogen (H):

H(g) → H+(g) + + e-

ΔH° = -1312.0 kJ/mol

Calculating the Ionisation Energy

We may use the following equation to calculate the energy ionisation potential of Hydrogen:

E = hcRH(1/n2)

where,

The electron’s energy is denoted by the symbol E (or the amount of energy it takes to remove the electron, Ionisation Energy)

h = 6.626 * 10-34 Js (joules*seconds) is Planck’s constant.

3.00 x 108 m/s (meters/second) is the speed of light.

RH is the Rydberg constant, equal to 1.097 * 107 m-1 (1/metres).

The electron’s primary quantum number (or energy level) is n.

After entering in the constant values, the equation becomes:

(2.18 x 10-18 J)(1/n2) = E

From here, you may fill in the value of the electron’s energy level to calculate the amount of energy required to remove it.

Conclusion

The ionisation energy, also known as the ionisation potential, is the amount of energy required to remove an electron from a neutral atom. It is the bare minimum for alkali metals with a single electron outside a closed shell. For the noble gases with closed shells, it normally increases across a row on the periodic maximum. 

For example, to ionise sodium, 496 kJ/mol or 5.14 eV/atom is required, whereas neon, the noble gas immediately before it in the periodic table, requires 2081 kJ/mol or 21.56 eV/atom. One of the key energy factors utilised in measuring chemical bonding is ionisation energy.

We can obtain any element’s ionisation energy by clicking on its chemical symbol in the periodic table.