Work is a physics term describing the amount of energy transferred when an object is moved over a distance by an external force, at least a portion of which is applied in the direction of displacement.
Work can be calculated by multiplying the length of the path by the component of the force acting along the path if the force is constant.
Mathematical expression for Work
Work is done on an object when a force works in or against the direction of motion of the object.
W=F△x cosθ
Here,
W = Work done in Joules (J)
F = Magnitude of force in newton (N)
Δx = Value of displacement in metre (m)
θ = angle between force and the direction of movement of the body.
Unit of Work
The S.I. Unit of work is considered as Joule(J).
For example, if a force of 10N is applied on a body and it is displaced by 15m at an angle of , then the work done will be
W = FΔx cos θ
W = 10 ✕ 15 ✕ cos θ
W = 75 J
Work done for different values of angle theta ( θ)
Now that we know about the mathematical expression of work, we should always keep in mind and consider the following factors while calculating work done.
The magnitude of the component of and is F cos θ . If the value of θ > 90° , the component will be parallel to the displacement direction but it points in the other direction, and the force opposes the motion.
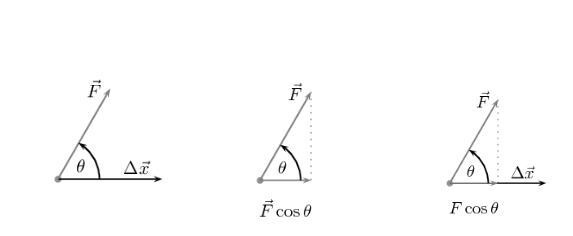
cos θ indicates the force’s relative direction as well as the displacement. The sign of the displacement vector and force vector will be different if the component of the force along the direction of the displacement is opposite in direction to the displacement. This is true regardless of which positive direction was picked.
Let’s look at some examples to better grasp these situations. The grey dot in the figures below symbolises an object. The object is acted upon by a force, . denotes the displacement of the object. In each situation, let us determine the sign of work done.
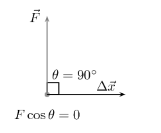
- At θ = 90° , cos θ = cos 90° = 0
- F cos θ = F cos 90° = 0
Therefore, work done is also ZERO.
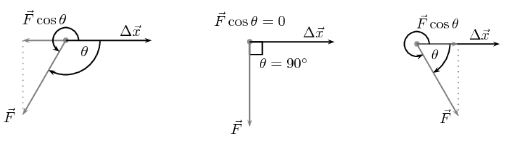
- At θ > 90°, the magnitude of the component of the force is along the displacement line in the opposite direction of the displacement.
Cos θ < θ
F Cos θ < θ
Therefore, the work done is NEGATIVE,

- It is necessary to keep in mind that for work to be done, a component of the applied force must be directed in the direction of motion. There is no work done by forces that are perpendicular to the direction of motion.
Scientific concept of work
When we apply force ‘F’ to a block, the body travels with an acceleration or its speed rises or declines depending on the direction of the force. The kinetic energy of the system changes as the speed increases or decreases. We know that energy cannot be created or destroyed, thus it must be changed into another form. It is referred to as work done in this situation. When negative work is done, the energy declines, and when positive work is accomplished, the energy increases.
Concept of heat and work
Heat: Consider a system that has both hot and cold parts within it. Conduction, radiation, and/or convection will transport energy from the hot to the cold region due to the temperature differential. Heat is exclusively given to energy transfer, not mass transfer, that occurs at the system’s surface. When the condition of the system changes, heat enters or exits the system. Heat isn’t a property, hence it doesn’t have a single value. The amount of heat that is transported is determined by the procedure (how the system moves from state 1 to state 2).
Heat is energy that is transported through the system’s surface via conduction and radiation methods.
Convection is not included since it involves a mass flow, and the energy associated with that mass will be examined separately. Heat is thus arbitrarily defined as a surface effect:
Heat is energy transported over a system’s boundary without the transfer of mass due to a temperature difference between the system and its surroundings.
Work: Work, like heat, is a transitory phenomenon that cannot be stored in mass or a system. Work is a surface concept that exists or occurs only during the passage of energy into or out of a system. After the work is completed, all that remains is the effort’s result: energy. Work into or out of the system happens as the system changes state, just like heat. Work is not a commodity, hence it cannot be single-valued. The procedure (how the system progresses from state 1 to state 2) determines the quantity of work transferred.
By paraphrasing the definition for heat, a general definition for all types of work may be formed:
Work is energy transported over a system’s boundary without the transmission of mass due to a significant physical difference between the system and its surroundings other than temperature.
Work Done for Thermodynamic Process
Isochoric, isobaric, isothermal, and adiabatic are the four basic thermodynamic processes. The following are the equations for work done in different thermodynamic processes:
1.Isochoric process: The isochoric process is defined as one in which the volume remains constant.
Δ V = 0
Since the volume change in an isochoric process is zero, the work done is also zero.
W = PΔV = 0
2.Isobaric process: The isobaric process is one in which the system’s pressure does not change (remains constant).
Δ P = 0
The formula for work done in an isobaric process is given as:
W = PΔV
3.Isothermal process: The isothermal process is one in which the system’s temperature remains constant.
Δ T = 0
The formula for work done in isothermal process is given as:
W=nRTln[V1/V2]
n = no. of moles of gas
R = universal gas constant = 8.3144 J.K-1.mol-1
V1 & V2 = initial and final volumes of the system
4.Adiabatic process: The adiabatic process is one in which the system’s heat energy does not change.
Δ Q = 0
The formula for work done in adiabatic process is given as:
W=1/1-ϒ[P2V2-P1V1]
ϒ=adiabatic index
P1 & P 2 = initial and final pressures of the system
V1 & V2 = initial and final volumes of the system
Conclusion
Work is the force that causes an object to move or be displaced. In the case of a constant force, it is the scalar product of the force applied on an object and the displacement induced by that force. Despite the fact that both force and displacement are vector values, it has no direction due to the nature of a scalar product.
Heat is energy transported over a system’s boundary without the transfer of mass due to a temperature difference between the system and its surroundings. On the other hand, Work is energy transported over a system’s boundary without the transmission of mass due to a significant physical difference between the system and its surroundings other than temperature.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out





