In the presence of an electric field, work has to be done to move a point charge from some point to another. The electric potential is the amount of work done in moving a point charge from one point to another against an electric field. Suppose we consider a positive charge q situated between two plates, 1 and 2, in the presence of an electric field E. As an electric field is present, the force will be exerted on the charge q, which is equivalent to F=qE. To move this charge, work needs to be done against this electric field, and for that, an equal and opposite force is to be applied, i.e., F= -qE. The work that needs to be performed to move this charge from plate 1 to plate 2 through some distance d will be W=Fd=-qEd. The SI unit of electric potential is joules per coulomb (volts).
Electric Potential Energy
Potential energy is defined as the energy possessed by a body by virtue of its height or position. In the case of electrical potential energy, charges exert forces on each other. As a result, potential energy arises due to the collection of charges. Let’s consider a positive charge q present at some point in the space. If another positive charge is brought closer, both of these charges will experience a repulsive force, and potential energy arises because of that force. The potential energy of a charge Q that is brought closer to the previous charge q will be given by
U = k Q q / r
where k is the coulomb’s constant.
And r is the separation between two charges.
Let’s discuss the variation of electric potential with the electric field. If a positive charge is moved against an electric field, the potential energy will increase. In contrast, if a positive charge is moved in the direction of the electric field, then the potential energy would decrease. In the case of a negative charge, the opposite variation takes place. Electric potential is path independent unless and until a charged particle crosses a magnetic field.
The difference in potential energies between two points gives us the work done in moving a charge from one point to another.
Electric potential due to a point charge
The basic segment of the matter is an electron, a point charge. You must be familiar with the charge distribution due to a metal surface. This spherical charge distribution creates an external field. Point charges create a similar external electric field. We need to discuss the electric potential in detail due to a point charge.
If electrostatic forces/powers are applied at a point in an electric field, the electric potential is characterised as a measure of the amount of work required to move a positive unit charge from infinity. Consider an electric charge at a point. Due to the presence of an electric field, the charge created by then applies power/force. Whenever r is a distance from the positive charge +q, the electric potential will appear as:
V = q/4πϵ0r
Where,
In a positive charge, r is the position vector
q is the source charge
Volts are the unit of electric potential,
1 Volt = 1 joule coulomb-¹
The electrostatic potential is supposed to be 1 volt at a point at which work is done by moving a charge of 1 coulomb from infinity to a specific point by means of an electric field against the electrostatic field.
Superposition of Electric Potential
Electric potential is a scalar quantity, and for a system of charged particles, we can simply add up potentials using algebraic laws. Consider a system of charged particles containing q1, q2, q3… at a distance of r1, r2, r3… from a point. Then, the potential at this point will be
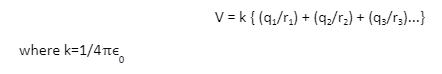
Problems
1. Find the potential at a distance of 5 m due to a charge of 4C.
Solution: Here, r= 5 and q= 4
Substituting the given values in the following equation, we get
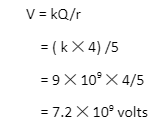
2. Find the potential at a distance of 1 m due to a charge of 5pC.
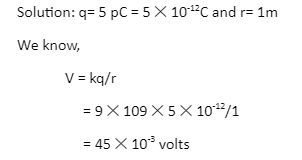
Conclusion
As you can see, electrostatic potential is a scalar representation of the region around a charge arrangement that is important for assessing the work required. Since electric charges surround themselves with fields, they have to undergo work if they wish to move. The energy that a charge makes when it moves is called its electric potential energy.The electric potential of a point charge is given by V = q/4πϵ0r. From this equation, we conclude that the farther we move a charged particle from the source, the electric potential will become lower and lower. The electric potential is zero at infinity. Also, the superposition principle is used to calculate the electric potential of a system of particles. If a positive charge is moved against an electric field, then the potential energy will increase. In contrast, if a positive charge is moved in the direction of the electric field, then the potential energy would decrease. In the case of a negative charge, the opposite variation takes place.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






