
Achieve your IIT dreams with Unacademy
Line charge is defined as charge distribution along a one-dimensional curve or line L in space.
In this article, we will find the electric field due to a finite line charge at a perpendicular distance and discuss electric field line charge importance. We would find the electric field through the derivation method without using Gauss’s Law.
Concept of electric charge
An electrostatic force acts between two charged bodies, even without any direct contact between them. The nature of this force is understood by introducing the concept of electric field.
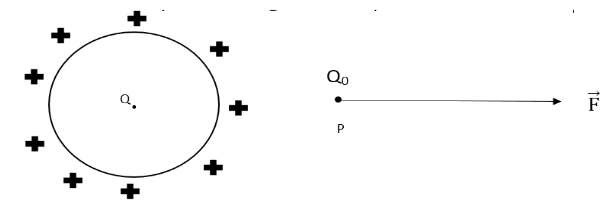
To test the existence of an electric field at any point P, simply place a small positive point charge Q0, called the test charge, at point P. If a force F is exerted on the test charge, an electric field E exists at point P and charge Q is called the source charge as it produces the field E.
An electric field is said to exist at a point if an electric force is exerted on a stationary charged body placed at that point. The electric field is defined quantitatively as the force experienced by a unit positive point charge placed at that point without disturbing the position of the source charge.

The electric field E is a vector quantity whose direction is the same as that of the force F exerted on a positive test charge.
Unit and dimension of the electric field
As the electric field is force per unit point charge, its SI unit is Newton per coulomb (NC-1). It is equivalent to a volt per metre (Vm-1).
The dimension for the field E can be written as

Where 1C = 1 A x 1s
The electric field due to finite line charge at the equatorial point
Consider an infinite line of charge with a uniform line charge of density . We have to calculate the electric field at any point P at a distance y from it. The total source charge Q is distributed uniformly along the x-axis between x = a to x = – a. We have to find the electric field due to the line charge at point P on the y-axis at a distance of y from the origin.
The diagram below is the representation of this explanation, and we have to derive the electric field formula at point P due to continuous charge distribution.
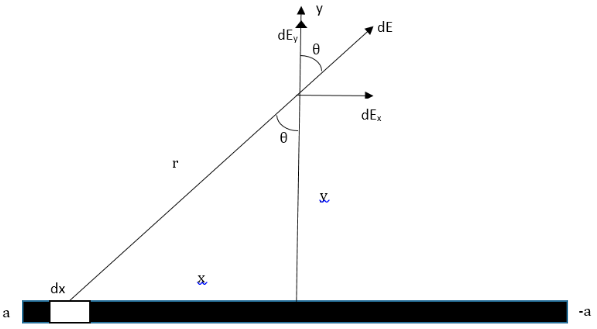
We solve this problem by breaking the line segment of length 2a into parts of length dx, with each of these parts carrying a charge of dQ. If the line charge density is ,
where =Q/a,
then from the diagram, we can see that the y-axis is the perpendicular bisector of the line segment. So, from the midpoint of the charged line segment, point P is at a distance ‘y’. Using Pythagoras Theorem, where r is the hypotenuse, x is the opposite side, and y is the adjacent side of a right-angle triangle, we can write,
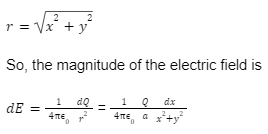
From the diagram, the component dEy is perpendicular to the charged line segment and dEx is parallel to the segment. So, resolving the component we get
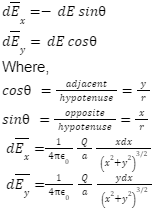
As the y-axis is the perpendicular bisector of the line segment, there is symmetry in the configuration. So, the component dE parallel to the line charge is zero. When a positive point charge (test charge) is placed at P, the perpendicular right-half of the charge line applies a force on the test charge towards the right side, while the left-half applies a force of equal magnitude towards the left side. Thus, the right and left parts of the segment contribute equally to the total electric field.
So, from symmetry dEx=0.
Thus, the total electric field at point P due to this charged line segment is perpendicular to it and can be calculated by finding the electric field on one side and then multiplying it with two, so we can get the total electric field in the region. For this, we have to integrate from x = a to x = 0. So,
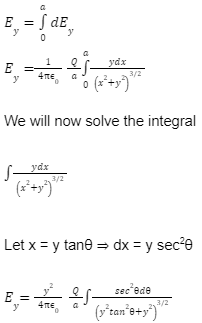
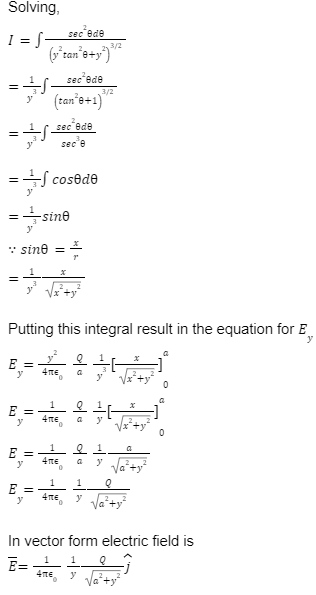
The electric field is directed away from the line charge if the rod is positively charged, and directed towards the line charge if it is negatively charged.
From the above equation, three cases arise


Conclusion
The electric field at a point is defined as the force experienced by a unit positive point charge placed at that point without disturbing the position of the source charge.

The electric field E is a vector quantity whose direction is the same as that of the force F exerted on a positive test charge. Its SI unit is Newton per Coulomb (NC-1).
The electric field due to finite line charge at the equatorial point is given by
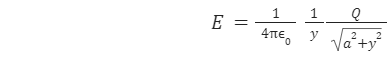
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



