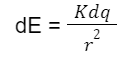Profile
Settings
Refer your friends
Sign out
An electric field is observed when a test charge (q) is held near a charge (Q) and it experiences some force of attraction or repulsion depending upon the positive and negative nature of that charge (Q). It was discovered by Faraday that every charge produces imaginary electric field lines that exert force on other charges placed in the vicinity of the given charge (Q).
NOTE: A source charge is a charge that produces the electric field, and a test charge is a charge used to test the effect of the source charge.
Electric Field
An electric field is defined as the region around a point charge in which its influence can be felt.
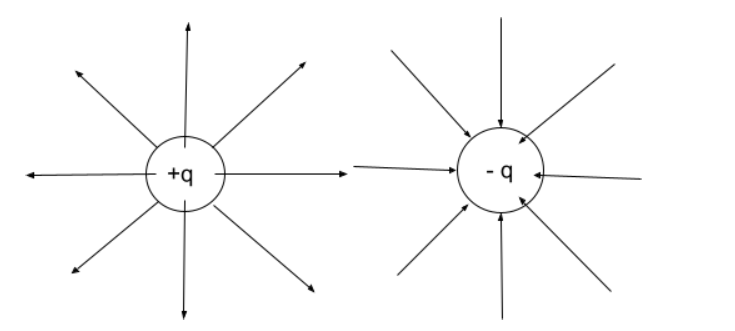
The direction of electric field lines is clearly shown in the above figures. For a positive charge, these are coming outwards. Whereas for a negative charge, these are going inward.
Electric field intensity
Electric field intensity is characterised by a vector function Ē. The electric field intensity due to point charge at a point is defined as the force experienced per test charge placed at that point.
Mathematically,
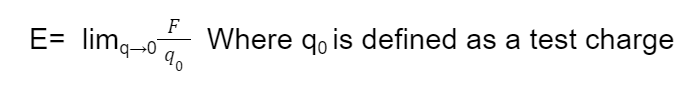
Electric field due to test charge is negligible compared to the electric field of source charge. As
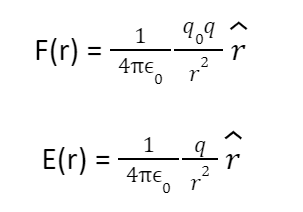
Where r is a unit vector from the origin to r. As a result, for each value of the position vector r, the above statement provides the electric field value.
Regarding electric field intensity, it is worth noting that-
It is a vector quantity having dimensions
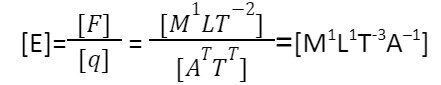
SI units are N/C or V/m.
As E is inversely proportional to the square of distance ‘r’ between charges, the electric field for a point charge is spherically symmetric.
It is valid only for point charges.
Electric field intensity due to charge at its own location is undefined.
What is charge distribution?
It is a distribution of the number of individual charges in a given space or a region.
Charge distribution is classified into two types:
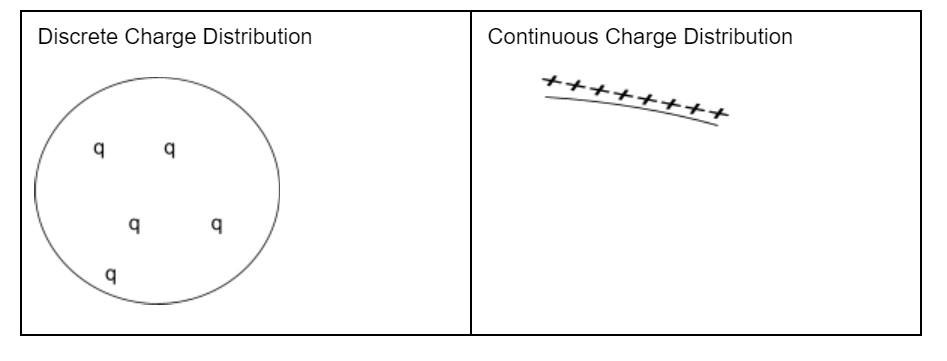
Types of continuous charge distribution
Consider charges q1, q2, q3 and q4 distributed in a given space and so on. It will be very difficult to calculate the electric field at any given point. That’s why three different forms of charge distributions are used.
1) Linear Charge Distribution
When charges are distributed linearly, for example, charges distributed on any given wire or any given curve,
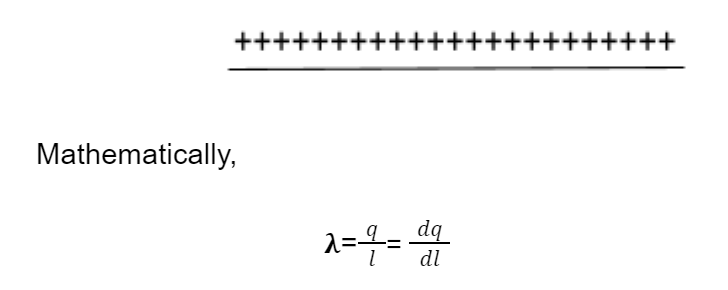
where dq is a small element on the given distribution.
* If the value of λ changes with the value of distance taken on the given distribution, it is said to be a nonuniform distribution. If the value does not change, it is said to be a uniform distribution.
2) Surface Charge Distribution
When charges are distributed on a given surface as shown below,
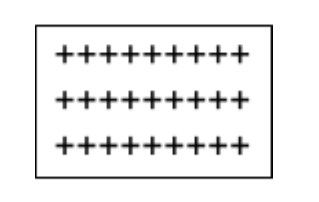
Mathematically,
𝛔 = q/A = dq/da
where dq is a small element on the given distribution and da is an area element on a given surface.
* If the value of σ changes with the value of distance taken on the given distribution, it is said to be a nonuniform distribution. If the value does not change, it is said to be a uniform distribution.
3) Volume Charge Distribution
When charges are distributed in a given volume as shown below,
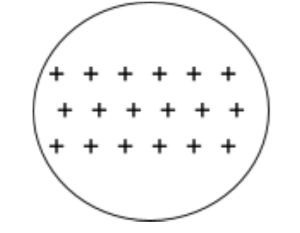
Mathematically,
𝛒 = q/V = dq/dV
where dq is a small element on the given distribution and dv is a volume element in a given volume.
* If the value of ያ changes with the value of distance taken on the given distribution, it is said to be a nonuniform distribution. If the value does not change, it is said to be a uniform distribution.
Electric Field Intensity due to continuous charge distribution
As explained above, total electric field intensity on a small test charge at any given point is given by,
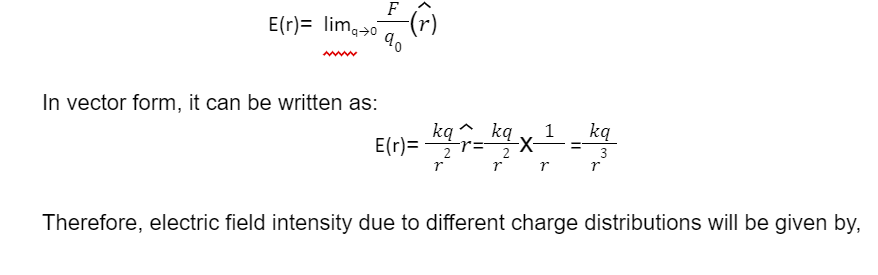
Electric field due to a charged ring on its axis
Consider a uniformly charged ring having a radius R with a point P on its axis at a distance x from the centre of the ring.
Consider dq as a point charge, then
For each dq, the values of r, R, x and θ will remain the same.
The dESinθ component of each dq is cancelled by dESinθ of the opposite element dq.
Now, we need to calculate the net value of electric field intensity.
E=∫dEcos𝞱
=∫(Kdq/r2)cos𝞱 = (K/r2)cos𝞱∫dq
As the total charge is Q and also,
r2 =x2 + R2
Now, equating above equation, we will get
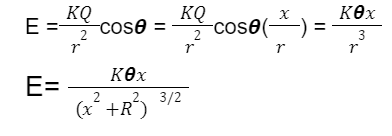
Conclusion
We have studied different types of distribution of charges and how to calculate electric field from the given charge distribution to any point in space. The electric field E is a vector quantity found at any point in the universe. If a test charge were placed in the field, then the force applied on that charge is represented by the electric field at that location. Electric field intensity can also be calculated by first calculating force and dividing it with the given test charge.
