Relation and Function

To better know the difference between relation and function, it is vital to know the concept of relation and function. 

• Two or more sets can have a relationship between them by any means and this is called relation
• For instance, consider there are two sets- Set A and Set B having elements m and n, respectively. Relation between any ordered pair can be built showing the relation between both the sets- Set A and Set B
• A function is capable of having the same range mapped as that of in the relation in such a way that a set of inputs is related to exactly one output
• For instance, in the example of two sets- Set A and Set B are related in such a way that all elements of Set A are related to exactly one element of SET B or it can be said that many elements of Set A are related to the one element of Set B. This particular type of relationship is referred to as function.

The above-mentioned statements clarify that a function can’t have one too many relations between given sets- Set A and Set B.

What is meant by Relation?

A relation in mathematics can be defined as the connection between the objects of two or more sets. It is the Cartesian product of the subsets that form the relation R. For instance, Set A and Set B have “a” and “b” as objects, respectively. It can be said that the objects are connected when the ordered pairs (a,b) are in relation.

Type of Relation:

Following mentioned are different types of relation:

• Empty Relation: This particular relation can be written as R = ∅
• Universal Relation: It is also referred to as a full relation because each element of Set X is related to each element of Set Y
• Identity Relation: In case each element in Set X is related to itself only then the particular relation is called identity relation
• Inverse Relation: In case there is a relation R from Set X to Set Y, R∈ X×Y, the inverse relation for same can be written as R-1 = {(y,x) : (x,y) ∈ R} 
• Reflex Relation: When each element of Set X maps for itself, the particular relation is referred to as reflex relation
• Symmetric Relation: A relation on the Set X can be referred to as the symmetric relation if (x, y) ∈R then (x, y) ∈R, such that for all x and y ∈ X
• Transitive Relation: A relation on the Set X can be referred to as a transitive relation if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R in such a way that for all x, y, z ∈ A
• Equivalent Relation: A relation on the Set X can be referred to as the equivalent relation if it is transitive, reflexive, and symmetric

What is meant by Function?

A function is referred to as a relation having one output for every input. In simple words, it can be said that it is a set of ordered pairs following the rule that each value of x is connected with only one value of y. 

Types of Function:

Following mentioned are different types of functions:

• One-to-one Function: also known as injective function, this particular function (f: X → Y) represents the distinctive value of Y for each value of X
• Many-to-one Function: This particular unction maps out two or more elements of X having the same element of set Y
• Onto Function: This particular function states that for each element of set Y there is a preimage in set X
• One-one and Onto Function: This particular function states that the function F matches with every element of X with a discrete element of Y. Also, for each element of set Y, there is a preimage in set X

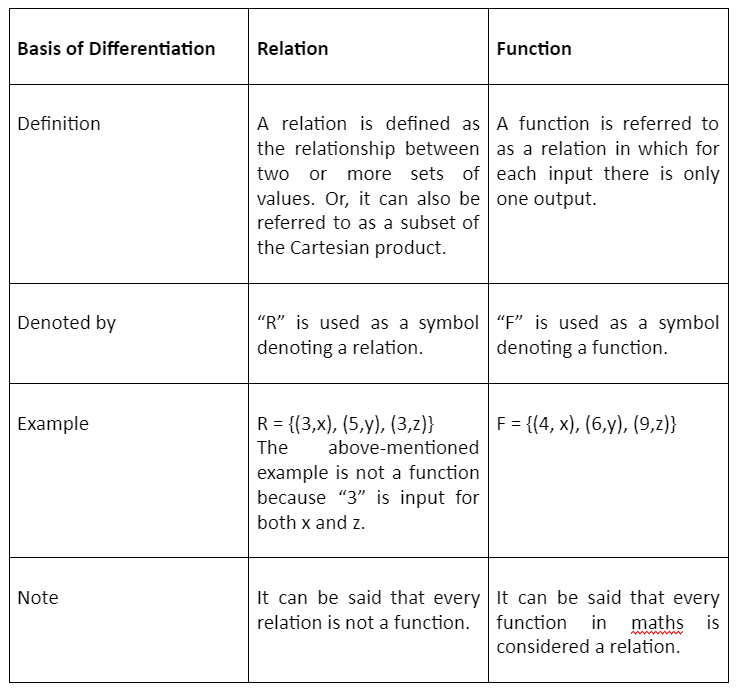
Understanding the difference between relation and function in the tabular form:

The following mentioned table comprises the difference between relation and function:

Conclusion

Relation and function are two vital concepts of mathematics that are closely related to each other. It can be complicated to differentiate between both of them. To learn about the difference between relation and function, it is suggested to go through the article as mentioned above.