Equilateral Triangle Formula

Equilateral Triangle Formula

In mathematics, sums regarding equilateral triangles, most of the formulas used are of the triangle, perimeter of the triangle, and the height of the triangle. 

An equilateral triangle is just a simple triangle in which all sides and all angles are equal, moreover, all the angles have a value of 60 degrees. In this article we would learn about the formulas that are applied in an equilateral triangle. Such as the area, height, and perimeter of the triangle. 

Area Formula

As we know that the area is the region covered by any 2d shape such as an equilateral triangle in this case. Although the formula we all know that is,

A = ½ × b × h

Where,

A = Area

b = base

h = height

Can be used in the equilateral triangle also when we know the height of the triangle. However, since we have the same values for the sides of an equilateral triangle a more simple and convenient formula has been derived in which directly we can put the value of the side and find out the area. 

The area of equilateral triangle is,

Area (A) = (√3/4)a²

Where,

a = equilateral triangle’s length of one side

Derivation of Area of Equilateral Triangle 

The thing that is curious to know is how the direct formula shown above can be derived. Let us derive the same. 

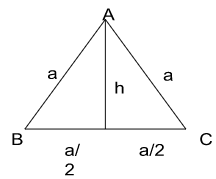
Consider the diagram and the annotations below,

We have a triangle ABC side A.

Now, the formula that we all know, that is,

A = ½ × b × h

Applying the pythagorean theorem in the same to find the value of h as we do not know it for now.

a² = h² +(a/2)²

h² = a² -(a/2)²

h² = a² -(a²/4)

h² = 3a²/4

h = √3a/2

Since we got the value of h, now applying the same in the formula we wrote above,

A = ½ × a × √3a/2

Here,

Base (b) = a

A = √3a²/4

Perimeter of the equilateral triangle

Again as we all know that the perimeter is the sum of all slides of a polygon. And the same applies for an equilateral triangle.

The formula for perimeter of an equilateral triangle is given by equation,

Perimeter (P)=sum of all sides

P = a+a+a

SInce all the sides are equal, which means a=a=a

Therefore,

P = 3a

Height of an equilateral triangle

Since most of the time only the sides of an equilateral triangle are given in mathematical sums, we may get into situations where we need to use or find the height of the triangle. Therefore, we must also know the formula for height of the equilateral triangle too.

So the formula for finding height of an equilateral triangle is given by equation,

h = √3a/2

Where

h = equilateral triangle’s height

a = side of the triangle 

The formula for height can be derived using the same method used to derive the formula of the equilateral triangle, which we’ve done above. 

Solved example

Find the area, perimeter as well as the height of an equilateral triangle having a side of 10 cm

Solving the question as,

Perimeter = 3a = 310= 30 cm

Area = √3a²/4 = √3 ×10²/4 = 25√3  cm²

And at the end,

Height = √3a/2 = √3 × 10/2 = 5√3 cm