Ellipse Formula:
- Ellipse is an integral part of the conic section and is similar in properties to a circle. Unlike the circle, an ellipse is oval in shape.
- An ellipse has an eccentricity less than one, and it represents the low of point, the sum of the two of the constant value
- A simple example of the ellipse in our daily life is the shape of an egg in a two dimensional form and the running tracking in a sports stadium.
- An ellipse if we speak in term of lows, it is the set of all points on a XY-plane whose distance from two fixed points adds up to a constant value
- The ellipse is one of the conic sections that is produced when a plane cuts the cone at an angle with the base. If the cone is intersected by the plane, parallel to the base, then it forms a circle.
Ellipse Shape:
In geometry an ellipse is a two dimensional shape that is defined along its axes. It has two focal points. The sum of the two distances to the local point, or all the points in the curve, is always constant.
Major and minor axis:
Ellipse is defined by its two axis along x and y axis:
- Major axis
- Minor axis
The major axis is the longest diameter of the ellipse (usually denoted by ‘a’), going through the centre from one end to the other, at the broad part of the ellipse. Whereas the minor axis is the shortest diameter of ellipse (denoted by b’)
Crossing through the centre at the narrowest part. Half of the major axis is called semi-major axis and half of the minor axis is called semi-minor axis.
Properties of an ellipse:
- Ellipse has two focal points also called focci
- The fixed distance is called a directrix.
- The eccentricity of ellipse, lies between 0 to 1. 0<_e<1
- The total sum of each distance from the lows of an ellipse to the two focal points is constant.
- Ellipse has one major axis and one minor axis and centre.
Ellipse formula:
The general equation of an ellipse is used to algebraically represent an ellipse in the plane. The equation of an ellipse can be given as
x² / a²+y² / b²=1
Parts of an ellipse:
let us go through few important terms relating to different parts of an ellipse
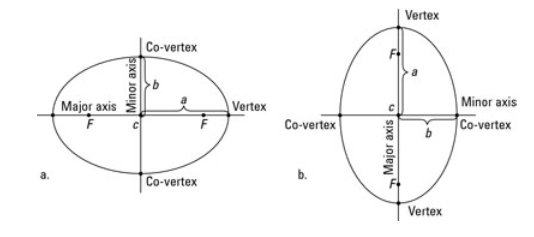
- Focus
- Centre
- Major axis
- Minor axis
- Latus rectum
- Transverse axis
- Conjugate axis
- Eccentricity
Example:1
What are the values of ‘a’ and ‘b’ in the equation of ellipse 16x2+25y2=160
We get, x² / 100+y² /64=1 with x² / a²+ y² / b²=1
The values are a= 10, and b=8.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



