Double angle formulas

This unit examines the double angle formulae, which are trigonometric. That’s because they engage trigonometric features of double angles, such as sin 2A, cos 2A, and tan2A.

Double angle equations are being used to express the trigonometry ratio of double angles in terms of single angle trigonometric ratios (). The double angle equations are special instances of (and thus derived from) the trigonometric sum formulas, as well as some alternate solution equations sourced through the Pythagorean terms. Let us review the trigonometry sum formulas.

• sin (A + B) = sin A cos B + cos A sin B
• cos (A + B) = cos A cos B – sin A sin B
• tan (A + B) = (tan A + tan B) / (1 – tan A tan B)

We will derive the sin, cos, and tan double angle formulas by replacing A = B for each of the above total amount formulas. We will also deduce some alternate solution formulas through Pythagorean terminologies. Here are double angle formulas, followed by their derivations.

1. Sin 2A = 2 sin A cos A = (2 tan A) / (1+tan2 A)
2. Cos 2A = cos2 A – sin2 A = 2cos2 A – 1 = 1-2sin2 = (1 – tan2 A) / (1 + tan2 A)
3. tan 2A = (2 tan A) / (1 – tan2 A)

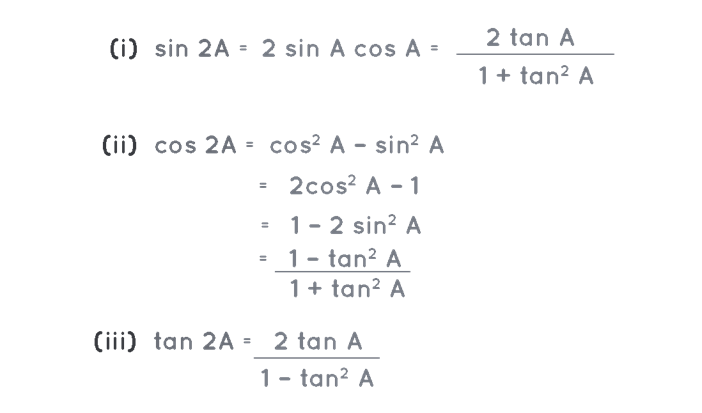
The sum method of sin feature is,

sin (A + B) = sin A cos B + cos A sin B

Once A = B, the overhead method becomes,

sin (A + A) = sin A cos A + cos A sin A

sin 2A = 2 sin A cos A

The sum method of the cos method is,

cos (A + B) = cos A cos B – sin A sin B

Once A = B, the overhead method becomes,

cos (A + A) = cos A cos A – sin A sin A

cos 2A = cos2A – sin2A

The sum method of tangent feature is,

tan (A + B) = (tan A + tan B) / (1 – tan A tan B)

Once A = B, the overhead method becomes,

tan (A + A) = (tan A + tan A) / (1 – tan A tan A) =(2 tan A) / (1 – tan2A)

Therefore, the double angle method of the tan formula is,

tan 2A = (2 tan A) / (1 – tan2A)

Solved Example

Consider the formula sin 3x. We would use the addition and double angle formulas to solve this problem.

Write it differently, using only terms related to sin x as well as its powers.

To begin, consider 3x as 2x + x and afterward apply an addition formula

3x sin = 2x + x sin

Using first addition formula, = sin 2x cos x + cos 2x sin x

Utilizing the double angle formula, = (2 sin x cos x) cos x + (1 2 sin2 x) sin x

1 2 sin2 x = cos 2x

+ sin x 2 sin3 x = 2 sin x cos2 x + sin x 2 sin3 x

= 1 sin2 x + sin x 2 sin3 x from the identification cos2 x + sin2 x = 1