Profile
Settings
Refer your friends
Sign out
Cone Formula
A cone is a 3D-shaped object with a circle at its base. A cone gets broadened as we go down and, in the end, it has a flat surface.
A cone is made up of a circle and a triangle. So, a cone has radius r, height h and slant height l.
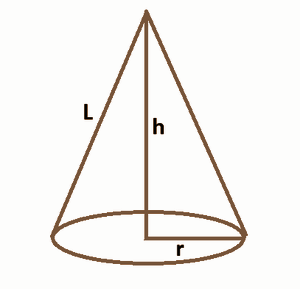
· Right angular cone
· Oblique cone
A right angular cone is a cone whose radius makes a right angle with its height. While an oblique cone is a cone whose radius does not make a right angle with its height.
In most of the cases, the cone is a right angular cone and so to find its slant height l is very easy, one can apply the Pythagoras’ theorem and find out the slant height of the cone.
l2 = h2 + r2
where, l is the slant height, h is the height and r is the radius of the cone.
The formula to find the surface area of a cone is
Surface area of a cone = r(l + r)
Where, r is the radius, l is the slant height of the cone.
The formula to find the volume of a cone is
Volume of a cone = 13r2h
Where, r is the radius and h is the height of the cone.
Examples:
1. A cone has the slant height l 5 cm and the height h 4 cm. Find the area of the cone.
Given data: l = 5 cm and h = 4 cm
To find the area of the cone, we would need radius r
So, to find radius, we would put the formula,
l2 = h2 + r2
52 = 42 + r2
25 – 16 = r2
r2 = 9
r = 3
We got radius = 3, now we can find area of the cone
Surface area of a cone = r(l + r) = 22/7 x 3(5+4) = 22/7 x 27 = 84.85 sq. cm.
2. A cone has a height h 14 cm and radius r 6 cm. Find the volume of the cone.
Given data: h = 14 cm and r = 6 cm
The formula to find the volume of the cone is
Volume of a cone = 13r2h = x 22/7 x 62 x 14 = 528 cubic cm.
Note: Surface area is always measured in square units. For example, sq. cm, sq. m, sq. feet, etc. And volume is always measured in cubic units. For example, cubic cm, cubic m, cubic feet, etc.
