What are the Real-Life Uses of a Square

A square is a type of quadrilateral that has all four sides the same length. There are a lot of things in our immediate environment that has a square form to them. Each square may be recognised by the fact that it has four equal sides and internal angles that add up to exactly 90 degrees. 

Square: 

A square is an example of a closed two-dimensional form (also known as a 2-D shape) that has four sides. A square has four sides that are each the same length and run parallel to the other sides. The fundamental outline of a square is depicted down below. 

A square is a quadrilateral in which:

• The opposite sides are parallel.
• All four sides are equal.
• All angles measure 90°. 

Properties of a Square: 

A square is a closed shape that has four sides that are all the same length, and all of the angles on the inside of a square are equal to 90 degrees. A square can take on many different appearances and behaviours. The following are some of the most important features that a square possesses.

1. A quadrilateral with four sides and four vertices is known as a square.
2. The lengths of each of the square’s four sides are identical to one another.
3. A square has four sides, each of which is perpendicular to the other three.
4. At each vertex, the inner angle of a square is equal to 90 degrees.
5. The total number of interior angles adds up to 360 degrees.
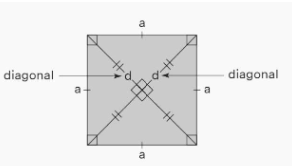
6. In a square, each of the four diagonals cuts the other diagonal at an angle of 90 degrees.
7. Each of the diagonals has the same amount of length.
8. A square is sometimes referred to as a parallelogram since its sides are parallel to one another.
9. In a square, the length of its diagonals is greater than the length of any of its sides.
10. The square is cut into two triangles that are identical to one another by the diagonals. 

Common Properties of a Square and Rectangle: 

Both a square and a rectangle share some of the same characteristics in many respects. The following list of points illustrates all of the characteristics that are shared by a square and a rectangle.

1. Both a square and a rectangle are examples of quadrilaterals, which are geometric shapes with four sides and four vertices.
2. The diagonal sides of a square and the perpendicular sides of a rectangle are parallel to one another.
3. Each angle on the interior of a square and a rectangle is equal to 90 degrees.
4. The inner angles of a square and a rectangle add up to a total of 360 degrees when added together.
5. A square and a rectangle can each be cut into two triangles with right angles by using the diagonal of the shape.
6. Due to the fact that the perpendicular sides of a square and a rectangle are parallel to one another, these two shapes are also referred to as parallelograms. 

Formulas of a Square: 

We are aware that a square is a figure that has four sides and all of the sides are equal in length. In geometry, there are three fundamental formulas that are utilised to solve problems with squares. The first formula is to determine its area, the second formula determines its perimeter, and the third formula determines the diagonal of a square. 

Area of a square: 

The amount of space that is taken up by a square is referred to as its area. The chessboard and the square wall clock are only two examples of square-shaped objects. To calculate the amount of space that these things take up in our environment, we can make use of the formula that describes the area of a square. The equation for calculating the area of a square is as follows: Area of square = s², where s is the length of one of the square’s sides. It is stated using square units such as cm², m², etc. 

Perimeter of a square: 

The complete length of a square’s boundary is referred to as the perimeter of the square. As a result, it is possible to determine the perimeter of a square by simply adding together the lengths of each of the sides. To get the perimeter of a square, we must first add up each of the four sides, as a square has four sides in total.

We may determine the length of the square’s boundary by applying the formula for calculating the perimeter of a square. Perimeter of a square Equals side + side + side + side. Therefore, the perimeter of a square equals four times the length of a side. Linear units such as centimetres, metres, and inches, among others, are used to express it. 

Diagonal of a square formula: 

A square’s diagonal is a line segment that unites any two of the square’s vertices that are not contiguous to one another. In the following square, the diagonals of the square are indicated by the letters AC and BD. It should be noted that both the line AC and the line BD have the same length. A square can be cut into two equal right triangles using a diagonal, and the diagonals themselves constitute the hypotenuses of the triangles that are formed when a square is diagonally cut.

Let us look at the process that is used to generate the formula for the diagonal of a square. Continuing with the example given before, we will refer to the length of a square’s side as “a,” and the length of its diagonal as “d.” A Pythagorean theorem is a useful tool for analysing the triangle we have here ADC: d² = a² + a²

Taking the square root of both sides results in the equation (d²) =. ( 2a²). Therefore, the formula for the diagonal of a square is as follows: The Diagonal of the Square, or d = √2 x a. 

Conclusion: 

The characteristics that constitute a square are that it has four straight sides that are all the same length and four angles that are all right. Examples of squares that can be found in the real world are windows (unless they are rectangles), coasters, the spaces on a chessboard, and the keys on a keyboard.