Indices are used to display how many times a number has been multiplied by itself. They can also be used to represent roots and fractions, such as the square root. The principles of indices make it possible to alter expressions involving powers more quickly than if they were written out whole.
We’ll start with the formal notation for writing a number with an index, then go on to the laws that govern it. So, let’s get started!
What are Indices used for
Exponents, index numbers, powers, and indices are all utilized in various aspects of modern technology. Exponents are utilized in a variety of fields, including computer game physics, pH and Richter Measuring Scales, science, engineering, economics, accounting, and finance, to name a few. Finance, Demographics, Biology, Economics, Resources, Electronics, and many more fields rely heavily on exponential growth. Light, sound, sporting goods, hazardous chemicals, and radioactive waste are all examples of exponential decay. Economists, bankers, financial advisors, insurance risk assessors, biologists, engineers, computer programmers, chemists, physicists, geographers, sound engineers, statisticians, mathematicians, geologists, and a variety of other professions employ exponents. We will demonstrate various real-world applications of exponents in this session, as well as their impact on our understanding of the modern world.
Constants and variables are used in algebra. A constant is a value that does not change. A variable quantity, on the other hand, can be assigned any number or have its value altered. We deal with indices in terms of numbers in algebra. Let’s look at the laws/rules of indices, as well as formulas and examples.
Application of Indices in Math
The little floating number that appears after a number or letter is called an index or power. Indexes is the plural form of index. The number of times a number or character has been multiplied by itself is represented by an index.
- . X²(Read as ‘X squared’) means X×X. X has been multiplied by itself twice. The index, or power, here is 2.
- . X³(Read as ‘X cubed’) means X×X×X. X has been multiplied by itself three times.
- .X4 (read as ‘X to the power of 4′) means X×X×X×X. X has been multiplied by itself four times, and so on.
- We must be able to employ the laws of indices in a number of ways in order to calculate with indices.
Applications are as follows:
Example: Given that 100.48 = x, 100.70 = y and xz = y2, then the value of z is close to:
xz=y2
⟹100.48z = 102×0.70 = 101.40
⟹z=140 / 48=35 / 12 = 2.9
Example: The value of 10150 ÷ 10146
(10)150 ÷ (10)146 = 10150/ 10146
= 10150-146
= 104
=10000
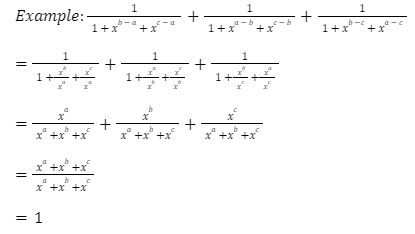
Indices Characteristics
An index can be assigned to a number or a variable. A variable’s index (or constant) is a value that is raised to the variable’s power. Indexes are also referred to as powers or exponents.
xn=x×x×x×x×………×xn times
Before we begin working with indexes, we must first understand certain fundamental principles or laws that govern them. These rules are applied while conducting algebraic operations on indices and solving algebraic equations, which includes it. Let’s have a look at the various methods for calculating with indices.
- If the index of a constant or variable is ‘0,’ the outcome will be one, regardless of the base value.>X0=1 for any value of x
- If the index has a negative value, the reciprocal of the positive index raised to the same variable might be used.>X-r= 1 / Xr
- We must sum the powers of two variables with the same base and raise them to that base to multiply them.>Xr.Xs=Xr+s
- To divide two variables with the same base, subtract the denominator’s power from numerator’s power and raise it to that base.>Xr/ Xs=Xr-s
- When a variable with one index is raised with another index, both indices are multiplied together and raised to the same base power.>Xrs=Xrs
- When two variables with different bases but the same indices are multiplied, the base must be multiplied and the same index must be raised to the multiplied variables.>Xr.Yr=XYr
- When two variables with different bases but the same indices are divided, the bases must be divided and the same index must be raised.>Xr / Yr=XYr
- The radical form can be used to indicate an index in the form of a fraction.>X r /s=s √Xr
Conclusion
Indexes are a valuable tool in mathematics for describing the process of raising or lowering a number to a power or root. Taking a root is the same as taking a fractional power of a number, but taking a power is the same as multiplying a number by itself numerous times. By estimating index numbers, you can create a single measure of change for a large number of items. Numbers, quantity, volume, and other factors can be used to calculate Index Price. The calculations also show that index numbers must be interpreted with caution. The products that must be covered, as well as the choice of a base time, are critical considerations. The importance of the index numbers cannot be overstated. It is critical, as indicated by the fact that it is necessary.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






