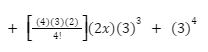In Statistical and Probability Analysis, the binomial theorem is commonly utilized. It is really beneficial because our economy is based on statistical and probability analysis. The Binomial Theorem is used in advanced mathematics and calculating to determine the roots of equations in higher powers. It’s also used to prove a lot of important physics and math equations. Weather forecast services, architecture, and cost estimation in engineering projects.
Binomial Theorem is Used in Real Life Situations
The forces of binomials that cannot be extended using algebraic identities are discovered using binomial expansion formulae. The binomial theorem is another name for binomial expansion formulas. A binomial is an algebraic expression with two terms.
Some exceptional no-use scenarios, such as computers and the automatic distribution of IP addresses for computer networking, appear implausible without this basic theory. Other industries that rely heavily on the binomial theorem include economic forecasting, where economists all around the world use it to forecast the growth of a country, a corporation, and other enterprises over the next few years.
Economy
The impact of the economy can be calculated using the binomial mathematical theorem, and a real-life example is the US economy, which bases a substantial portion of its operations on probabilistic analysis. The binomial theorem can be used to forecast how a country’s economy will perform in the near future. It is quite valuable in terms of making accurate economic forecasts.
Because we are anticipating the future state of the economy based on present facts and insights, this research is also known as Economic Forecasting.
Higher mathematics
The binomial theorem is a mathematical formula that is used to perform extremely difficult and practically impossible calculations. Binomial theorems were used extensively in several of Sir Albert Einstein’s equations, laws, and theories. If you want to use the Binomial Theorem in more advanced scenarios, your current knowledge of mathematics may not be sufficient, or if you are already willing to learn more advanced mathematics, the concepts of this theorem will be extremely useful for any type of research, mathematical analysis, or projects.
Ranking
The binomial theorem is used to determine scores and ranks when you take an exam and wait for the results so you can get into the college of your choosing or obtain a scholarship for your study.
The binomial theorem is also used to compute the various national rankings we get based on various indexes. So, the next time you see a ranking based on specific measures or parameters, you can be confident that the binomial theorem is being used.
Internet protocol (IP)
The power of the binomial theorem may simply be used to generate and distribute IP addresses to an ever-increasing number of electronic devices, which have grown tremendously in the last decade thanks to the boom in businesses such as the Internet of Things (IoT). Not only that, but you can programme it to calculate its own time and cost for completing a task. Variable subnetting is the name of this technique, and it is widely utilised in the sector.
How is binomial theorem used in forecasting?
It can be applied to weather forecasting. It is essential for forecasting and understanding weather trends. We can use the existing data to forecast the weather for the next few days or weeks using the existing data. If we consider it, this has had a huge impact on our lives. We don’t normally go on vacations if the weather prediction predicts rain, demonstrating how important such concepts are in our daily lives without us even recognising it.
The binomial theorem can also be used to forecast impending disasters. This has the potential to save lives and is necessary in our daily lives. We can save a lot of people’s lives from calamities like tsunamis and cyclones.
Binomial theorem The Binomial Theorem is a technique for expanding an equation raised to any finite power. A binomial Theorem is a useful expansion technique that can be used in Algebra, probability, and other fields.
According to the binomial theorem, any non-negative power of binomial (x + y) can be expanded into a total of the form,
Also see: CAT Previous Year Papers
Conclusion
Binomial For a positive integral exponent n, the theorem can be used to expand the binomial (a+b) algebraically. The calculation becomes difficult and time-consuming as the power of an expression grows. So, even the x20 coefficient may be easily calculated using this reasoning. In the case of a random experiment, the theorem is extremely useful in determining the probabilities of events. The Binomial Expression is a mathematical expression made up of two terms that include addition and subtraction operations.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out