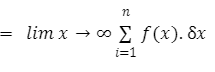Area under the Curve Formula

Area under the Curve Formula:

 The area under the curve is found by knowing the equation of the curve, the boundaries of the curve, and the axis enclosing the curve.

The area under a curve between two points is found by doing a definite integral between the two points. 

To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. This area can be calculated using integration with given limits. The process of integration used to solve the equation and find the area.

The area under the curve is the area bounded by the curve, the axis, and the boundary points. The area under the curve is defined as a two-dimensional area, which has been calculated with the help of the coordinate axes and by using the integration formula.

The area under the curve can be calculated approximately by breaking the area into small parts like small rectangles.

The area under the curve can be calculated using three methods.

Method 1:  The area under the curve is broken down into the smallest possible rectangles. The formula for the area under the curve is A

Method 2: This method also uses a similar procedure as the above to find the area under the curve. Here the area under the curve is divided into a few rectangles.

Method 3: This method uses the integration process to find the area under the curve. For a curve having equation y=f(x), and bounded by the x-axis and with the limit values of a and b, the formula for the area under the curve is A=_a^bf(x)dx.