Area Of Hexagon Formula

Area of a hexagon can be found by using two formulas which are mentioned in this article in detail. Read out the article to understand more about the area of hexagon formula. 

Introduction

A hexagon is a polygon which contains 6 sides as its name suggests the is derived from Greek words that are “Hexa” the meaning of which is six and “gonia” the meaning of which is corners. In a combined way that is called a six corners polygon. Here, all the sides and corners/angles are equal. And the angles have a value of 120 degrees. 

Area of Hexagon

As we all know that the area is the region enclosed in the particular polygon, here in the case of the hexagon is also the same. A hexagon is a polynomial having 6 sides, 6 angles and 9 diagonals. Moreover the sum of all angles comes out to be 720 degrees. The units for measurement of area of a hexagon are m2, cm2, mm2, ft2, inch2, etc. in whichever units it is required, the unit is squared and we get the unit of its area. 

The formula for the area of a hexagon can be written as,

Area (A)=33s22

Where,

s = side of the hexagon given.

Derivation of Area of Hexagon

After we got to know the formula for the area of a hexagon, we are curious to know how that particular formula is derived. So, let us derive the same.

The first step in deriving the formula for a regular hexagon is drawing the same in a sheet of paper as shown below,

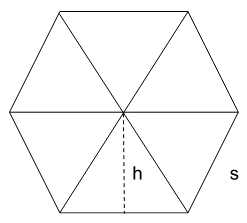
Now, that we’ve drawn a hexagon, we need to divide it into 6 equal triangular parts as shown below,

Also, annotate the height of the triangle and side as shown.

Now,

As we all know the basic formula for area of a triangle which is ,

A=12bh

Substituting the values as 

b = s (side of hexagon)

And h = h (height of the triangle formed in the hexagon)

Therefore,

A=12sh

Now, since, we have 6 similar triangles inside a hexagon. Thus, the area of the hexagon becomes equal to 6 times the area of one triangle into the hexagon. Mathematically depicting the same as,

A=612sh

A=3.s.h

Now, we need to find the value of h using pythagoras theorem,

h2=s2-(s2)2

h=32s

And at the end when we apply the same value of h in the formula of hexagon obtained we get the equation as,

A=3.s.32s

A=33s22

Area of a Hexagon Using Apothem

Sometimes the radius of the hexagon is also given, and we can also get another formula using the same. Here the radius of the hexagon is called the apothem. We can also understand it by taking it as the height of one triangle inside the hexagon. 

The formula for the area of a hexagon using apothem is as,

A=12ApothemPerimeter

And the perimeter of the hexagon can be found out by

Perimeter (P)=ssssss=6s

Solved Example

Find the area of a hexagon having side of 10 cm 

For that we simply use the formula, 

A=33s22

And substitute the value of s which is equals to 10 cm 

A=33*1022=1503 cm