Area of a Kite Formula

Area of a kite formula

The types of polygons that have four sides, four vertices, and four angles along with a pair of diagonals are referred to as quadrilaterals. There are some special types of parallelograms like rectangle, square, rhombus, kite, etc.

• A special quadrilateral in which each pair of consecutive sides is congruent, but the opposite sides are not congruent is called a kite. Angles between unequal sides are equal.

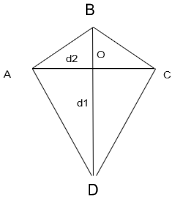
• The kite can be represented as a pair of congruent triangles with a common base.

• The diagonals of a kite intersect each other at right angles.

• The longer diagonal is said to be the perpendicular bisector of the shorter diagonal.

Derivation

BD = Long diagonal and AC = Short diagonal

The Figure given below, 

Derivation of Area of the Kite

Let, 

the long diagonal BD = d₁  

the short diagonal AC = d₂,

AC = AO + OC = d₂

Area of kite ABCD = Area of ΔABD + Area of ΔBCD… (1)

We know that,

Triangle’s Area = ½ × Base × Height

Now, let us calculate the areas of triangles ABD and BCD

Area of ΔABD = ½ × AO × BD = ½ × AO × d₁

Area of ΔBCD = ½ × OC × BD = ½ × OC × d₁

Therefore, by using (1),

Area of kite ABCD = ΔABD + ΔBCD

That is 

ΔABCD= ½ × AO × d₁ + ½ × OC × d₁

= ½× d₁ x (AO + OC)

= ½ × d₁ x d₂

Therefore, Δ ABCD = ½ × d₁ x d₂

Thus, we need to just multiply both the diagonal values and divide them by 2, when both diagonal values are given, to get the area of the kite.

Let us take some examples of the Area of kite formula

1) A kite with an area of 126 cm² has one of its diagonals that is 21cm long. Find the length of the other diagonal.

Solution: Given,

Area of a kite =126 cm²

Length of one diagonal = 21 cm

Area of Kite =

D₂ = 12cm

2) Given the larger diagonal, it is twice the smaller diagonal.

What is the relation between the area and the smaller diagonal of a kite?

Solution:

Let us assume that

the smaller and larger diagonal be d and 2d respectively.

Consider the area of the kite to be A.

Thus, we can write as

A = 1/2 × d × (2d)

A = d²

Thus, the area of the kite is the square of the smaller diagonal.