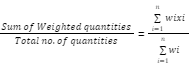Types of Averages and their Significance

Average is among the fundamental concepts in mathematics and is used in various equations and other mathematical purposes. It is a basic concept used in almost all fields of science, geography, astrology and more. Besides, it has found immense significance in subjects like statistics and commerce. There are different types of averages, and each type is used depending on the desired value from a group of numbers. 

What Is Average?

The mean value of a set of values is simply the ratio of the sum of the number of values in the set to the total number of values in the set. 

For example, if we need to calculate the average age of women or men in a group or the average adult height in India, we add all the numbers together and divide by the number of data.

Types of Averages

Here are the types of averages with their use cases:

Mean

The average of a set of values is known as the mean. It refers to a data set’s values being distributed evenly. The three most popular measures of central tendency are the mean, median, and mode. To find the mean, add all of the total values in the data and divide the total by the number of values of the data.

The formula used to calculate the mean is as follows: 

Mean = Sum of all quantities / No. of quantities

Example of a mean  

Consider the following numbers: 

23, 44, 64, 78, 21, 90. 

To find the mean of these numbers, we shall use the formula, 

Mean = Sum of all quantities / No. of quantities  

= 23+44+64+78+25+90 / 6 

= 54

Therefore, the mean of the given values is 54.

Weighted Average or Weighted Mean

A weighted average is a method that considers the relative value of the integers in a data collection. Each quantity in the data set is multiplied by a predefined weight before the final calculation is made when calculating a weighted average. 

The weighted average is calculated in mathematics and statistics by multiplying each integer in the set by its load. Then, the products are added, and the final amount is divided by the sum of all weights.

The formula for weighted mean is,

Weighted Mean

Example of a weighted mean

Consider 2 values –  40 kg at 60 rupees/kg and 25 kg at 32 rupees/kg. Therefore, the weighted mean would be – 

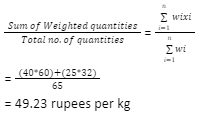
Median

In an ordered list of numbers, the median is the number in the middle. To find the median value in a set of data, sort them into values either from lowest to the highest or highest to lowest. The median could be used to estimate an average or mean, but it should not be mistaken with the true mean. 

The formula of a median is given as: 

Median = X(n / 2)  (if n is even)

or

Median = X(n-1 / 2)+X(n+1 / 2) / 2  (if n is odd)

Where, 

• X = Ordered list of values in a data set
• n = no. of values in the data set.

Example of a median

Consider the following numbers,

45, 24, 72, 12, 86, 63, 94, 50, 75, 100

By arranging the numbers in ascending order, we get, 

12, 24, 45, 50, 63, 72, 75, 86, 94, 100

Since the number of quantities is even, the formula used will be: 

Median = X(n / 2)

Since n = 10, we have a pair of middle numbers in the list, i.e ., 63 and 72.

Median = 63+72/2 

= 67.5

Therefore, 67.5 is the median number of the list.

Mode

The value that appears most frequently in a set is known as the mode. Apart from the mean and median, it is one of the main measures of central tendency. That is to say, the mode or modal value is the number or number in a data set that appears more frequently.

The formula of a mode is,

Mode – Grouped Data = L+h (fm-f1) / (fm-f1)+(fm-f2)

Where, 

• L is the modal class’s lower limit, 
• h is the class interval’s size
• f_m is the modal class’s frequency
• f₁ is the frequency of the class preceding the modal class
• f₂ is the frequency of the class succeeding the modal class

For ungrouped data, arrange the values in ascending order and look for the most repeated value.

Example of a mode

Consider the following values:

23, 45, 52, 74, 52, 23, 42, 78, 52, 70, 50, 52, 36, 61, 52, 70

Out of these groups of numbers, 52 is the most repeated number in the list. Hence the mode of the list is 52.

Conclusion

Mean, median, and mode all have unique use cases that are required in daily life. Median and mode are commonly used in statistics, whereas mean is the most common type of average used in almost every field. It is important to know the differences between these types of averages and use them accordingly.