Solving Area of Quadrilateral Related Problems

A quadrilateral is described as a polygon that embodies four sides (edges), four vertices (corners), and four angles. The term ‘quadrilateral’ was inspired by a Latin phrase that translates to ‘four sides’. It is also known by a synonym – tetragon. This term was inspired by the Greek language, where the phrase ‘tetra’ translates to ‘four’ and the phrase ‘gon’ translates to ‘side’. If the sides of a quadrilateral are named A, B, C, and D, the quadrilateral is illustrated as ABCD. There can be two types of quadrilaterals – simple and complex. Simple quadrilaterals do not self intersect while complex quadrilaterals self intersect. The area of a quadrilateral is described as the region that is enclosed by the quadrilateral. In the further sections, we will look at the properties and the various methods that can be used to calculate the area of quadrilaterals and the formula for the Area of quadrilaterals. 

Characteristics of quadrilateral 

There are six fundamental types of quadrilaterals – rectangle, parallelogram, trapezoid, square, kite, and rhombus. Although each of them has separate properties of their own, all of them have a few common characteristics. They are 

• They all have four sides 

• They all have four vertices

• They all have two diagonals present 

• The summation of all interior angles is always equal to 360 degrees.

What are the simple methods for problems involving quadrilaterals?

The methods that will be discussed in this section are 

• By dividing into two triangles 

• By using sides 

• By using Heron’s formula 

• If the quadrilateral is one of the fundamental types, then the direct area formula for that quadrilateral can be applied 

Finding the area of the quadrilateral by splitting the quadrilateral into two triangles 

In this method of solving for the area of the quadrilateral, the quadrilateral is split into two triangles. Then, the area of triangle formula is applied to the two triangles to obtain the final area of the quadrilateral. 

Problem: Consider a quadrilateral LMNO having side MN = 15 m, heights of each triangle LMO and MNO are 6 m and 8m. Calculate the area of this quadrilateral. 

Answer: Given – diagonal = 15 m, h1 = 5m, and h2 = 8m 

Here, we use the area of triangle to the two triangles 

LMO = ½ x 15 x 6 = 45 m2

MNO = ½ x 15 x 8 = 60 m2

The formula of Area of quadrilateral  is LMN + MNO = 45 + 60 = 105 m2

Finding the area of quadrilateral by using the length of sides 

This method is used when the two opposite angles along with sides are given. In this case, we can use Bretschneider’s formula. Consider that θ₁ and θ₂ are the opposite angles and the sides have a measured value of p,q,r, and t. The formula of Area of quadrilateral  is given by 

Here, s denoted the perimeter of the given quadrilateral that is analysed by

θ = θ₁ + θ₂

Problem: Consider a quadrilateral PQRT, whose sides have measured values of 6m, 4m, 8m, and 10m respectively and opposite angles 40 and 80 degrees. Analyse and elucidate the region enclosed by the quadrilateral.

Ans: The perimeter = 

= 14m and = 120 

Applying the formula of Area of quadrilateral 

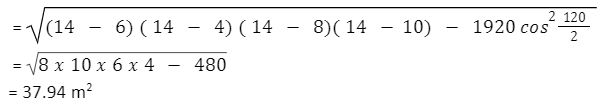
Finding the area of quadrilateral by Heron’s formula 

Heron’s formula is usually used for triangles. Consider p,r, and r as sides of a triangle, then the formula is

Here, s is called the semi perimeter of the triangle that is calculated by

To implement this formula for a quadrilateral, the quadrilateral must be divided into 2 triangles along its diagonal and this formula must be separately applied. Then, both the triangles are added to become the formula of the area of the quadrilateral. This formula is used only when the sides of a quadrilateral are given

Problem: Consider a quadrilateral PQRT with sides PQ =10m, QR =6m, RT=4m, and TP= 2m. The angle made at TPQ = is 90°. 

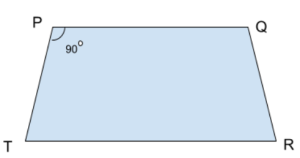
Answer: We can convert the quadrilateral into one right-angled triangle and one regular triangle as the angle is unknown. Hence, we can apply the Pythagorean theorem for the first triangle. 

For Triangle PQT  PQ2 + TP2 = QT2 

Area of PQT = ½ x 10 x 2 =  10 m2(TP is the height)

For triangles QRT, semi perimeter = 11 m 

Final area of quadrilateral is 17.65 + 10 = 27.655 m2 

The area formula for common quadrilaterals

• Rhombus: ½ x p x q. Here, q and q are diagonal 1 and diagonal 2 respectively

• Trapezoid: ½ x (c+d) x h . Here, c and d are the bases of the trapezoid and h is the height

• Parallelogram: B x H. Here, B notes the base and H is the height of the parallelogram

• Square:  p x p . Here, p denotes the length of a side of the square

• Kite:  ½ x p x q. Here, q and q are diagonal 1 and diagonal 2 respectively. Similar to rhombus

• Rectangle: l x b. Here, l denotes length and b denotes breath of the rectangle

Conclusion

In this article, we have elucidated the answer to the question – what are the simple methods to problems involving quadrilaterals?. A quadrilateral is a polygon that embodies four sides. It has four angles, four vertices, and four sides. Two kinds of quadrilaterals are available – simple and complex. The difference between them is that simple quadrilaterals do not self intersect while complex quadrilaterals self intersect. The area of a quadrilateral is described as the entire region occupied by a quadrilateral. There are 4 ways to calculate area – by using the sides, by using Heron’s formula, by splitting it into 2 triangles, and by directing using the standard formula for the common quadrilaterals.