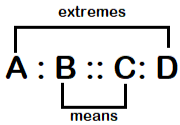Ratio and Proportion

Students’ understanding of numerous areas in mathematics and science depends on their ability to use ratios and proportions. They play a crucial role in the development of slope, constant rate of change, and other concepts and abilities essential to understanding and mastering algebra. Both ratios and proportions are based on fractions and help solve several day-to-day problems like comparing distance, weight, and height.

Ratios

It can be defined as the relationship between two variables.

If A=40 and B=20, what is the ratio A: B=?

            We can write it as A: B,

                           40:20 = 40/20=2/1

Hence, A: B=2:1

Even when multiplied by 2 on both sides of the ratio,

            A: B=(2×2):(2×1)

                  =4:2

                  =2:1

Still, the ratio will remain the same.

Proportions

It describes the comparative relation stating they are equal.

Eg= as given in the previous, we saw that

        A: B = 4:2=2:1.

Hence, it shows the proportion that they are equal.

Ratios and Proportions Formula

Now, we will discuss some methods for solving ratios and proportions.

1. Prime Ratio

A: B=2:1,

Even when multiplied by 2 on both sides of the ratio,

            A: B=(2×2):(2×1)

                  =4:2

                  =2:1,

the ratio will remain the same.

The ratio of A: B=2:1 is known as the Primary Ratio.

2. Dividing ratio with 1

Take A: B=3:1

Now, divide it by 1.

We get

      A/1 :B/1=3/1 :1/1

The prime ratio is still 3:1

Hence, even though you divide the ratio by the same numbers on both sides, the prime number remains the same.

3. Exponents and Means:

The ratio between the mean and the ratio between the extremes may be asked. It can be represented as

A/B :C/D= (AxD)=(CxB)

4. Componendo and Dividendo

If A/B :C/D , then the formula is

(A+B)/(A-B) :(C+D)/(C-D)

Example1: if A: B=2:3 and B: C=3:4. Find A:B: C.

Soln: Method 1-

              A: B=2:3 and

              B: C=3:4, since B is a common number so easily it can be written as

              A: B: C=2:3:4

 Method 2- General Formula

              This can be applied even if B is the same or not and is applicable for both,   

By this formula we get,

              (AxB) : (BxB) : (BxC)

               6:9:12

              Hence, 2:3:4 is the ratio for A:B: C

Example2: If X: Y=3:4 and Y: Z=8:9, find X: Z ?

Soln: Given that X: Y=3:4 and Y: Z=8:9

          Now we know the concept from the previous example

          Applying it we get

          X: Z=(3×8):(8×4):(4×9)

              = 24:32:36

              =6:8:9

         Hence X:Y: Z=6:8:9,

         So, we can write it as X: Z=6:9

         Also, X: Z=6:9

         X: Z=2:3 is the required ratio

NOTE: Remember the Inverted N trick for this kind of question.

Example3: If A: B=2:3 and B: C=4:5 and C: D=6:7 find A:B: C:D?

Soln: In this, we will have to use a different approach with a slight touch from the above concept,

In this, we got to remember the arrows, and we get the following formula,

Now applying this formula, we will get:

            (2x4x6):(3x4x6):(3x5x6):(3x5x7)

             16:24:30:35=A:B: C:D is the required ratio.

Example4: Divide the 600 in the ratio of 2:3?

Soln: We can write as a sum of the ratios,

                  2X+3X=600

                    5X=600

           Hence we get, X=120

Now multiply, 2X= 2×120  and  3X=3×120

                         2X=240                3X=360

The ratio we get is 240:360

Now the primary ratio will be 2:3

NOTE: If we want to cross-check then just add the two ratios we will get the sum which should be equal to the given sum,

                      240+360=600

                               600=600

                        So, LHS=RHS

So the calculated ratio is correct.

Example5: If A/2 :B/3 : C/5 , then A:B: C ratios will be?

Soln: We are given that the ratios A/2:B/3:C/5 = X

             So we can write it as A=2X

                                                   B=3X

                                                   C=5X

                                       A:B: C = 2X:3X:5X

          So the final required ratios is 2:3:5=A:B:C

Difference between Ratios and Proportions

Conclusion

• Ratios show the general relationship between any given number of variables.

• Proportions show that the two ratios are equal.

• When a ratio is multiplied by the number, its primary ratio will remain the same.

• For ratios like A: B and B: C, to find B: C, always use the inverted N method.