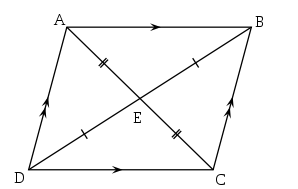
In the above picture, AD=CD and AB=BC and ∠B= ∠D and ∠A=∠C. ∠A+∠D+∠B+∠C= 360°. In this picture Angle B, Angle C, and Angle D, Angle A are known as supplementary angles because they remain on the same side of the parallelogram. 

Properties of parallelogram

A parallelogram is a special type of polygon because it has opposite facing sides. The properties of a parallelogram are discussed below:

• In a parallelogram, the angles of the opposite sides are congruent.
• Both the opposite sides of a parallelogram are of equal length. 
• Consecutive angles of a parallelogram are supplementary. 
• The two diagonals of a parallelogram bisect each other.
• If one angle of a parallelogram is right, then all of the angles are right. 

Formula of parallelogram

The parallelogram formulas are discussed below. 

Parallelogram Area

The formula for the area of a parallelogram: Area= Base * Height. 

Perimeter of parallelogram

The perimeter of a parallelogram is defined as the total distance of the boundaries of a parallelogram. For the calculation of the value of the perimeter, the value of the breadth and length of a parallelogram have to be known. 

P= 2 (a+b), where p is the perimeter, a is the slant length of a parallelogram and b is the base. 

Types of Parallelogram

Three types of parallelograms are included. They are rhombus, rectangle, and square. All these are special kinds of parallelograms. 

Rhombus

Rhombus is a special type of parallelogram. In a parallelogram, all the diagonals intersect at an angle of 90 degrees. It is the fundamental characteristic of a rhombus. The structure of a rhombus is similar to a diamond shape. Both the facing sides or opposite sides and angles are equal. 

Rectangle

Rectangle falls under the special category of a parallelogram. The rectangle is a two-dimensional structure that has 4 corners and 4 sides. All the opposite sides of a rectangle have a similar amount of length. The total of all the interior angles of a rectangle is 360 degrees. 

Square

Square is the last special kind of parallelogram. It is a 2D figure that contains four equal sides and the four angles of a square are equivalent to 90 degrees. The characteristics of a rectangle are almost the same as a square. The basic difference between these two is that all the four sides of a square are of the same length and the rectangle with its opposite sides are of equal length. 

Angle of parallelogram

A parallelogram contains a total of four angles and the sum of all the interior angles is equal to 360 degrees. The successive angles of a parallelogram are known as supplementary angles and the opposite angles are equivalent.

Parallelogram shape

It is a two-dimensional shape that has 4 sides, where the opposite sides are of the same length. If an angle of a parallelogram is correct, then all the angles are correct.  According to Euclidean geometry, a parallelogram is quite simply a quadrilateral having 4 parallel sides. Along with the two-dimensional (2D) shape, it also poses a 3d shape that is called parallelepiped. 

Difference between Rhombus and   Parallelogram

The main differences between these two are: all the four sides of a rhombus are similar whereas only the opposite sides are parallel in a parallelogram. The area of a parallelogram is a=bh and the area of a rhombus is A=d1d22. The perimeter of a rhombus and parallelogram is P=4a and P=2(a+b). 

Parallelogram example

An example on parallelogram is given below:

Example 1

Find out the total area of a parallelogram having a base and height of 6cm and 9cm. 

Area= Base * Height

Area= 6*9

Area= 54 `square cm.

Conclusion

The parallelogram is an important chapter in mathematics. For the proper understanding of this chapter, one must go through the concepts of the parallelogram. In this study, the overview of the parallelogram is discussed based on its definition, shape, properties, types, formulas.