Profile
Settings
Refer your friends
Sign out
A triangle is a geometrical figure with three sides that encloses an area. The sum of the interior angles of a triangle is equal to 180 degrees. The exterior angle of a triangle is equal to the sum of the two interior angles opposite to it. The area of a triangle can be calculated using many formulas. Still, the most straightforward and easy way includes taking any one of the three sides as the base and knowing the vertex’s height opposite to it. If we have both of these data, then the area can be easily calculated by using the formula:
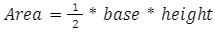
Another way of calculating the area of a triangle is by using Heron’s formula.Using Heron’s formula is a bit lengthier and more complicated method, but is extremely important in many cases. We will talk about both these methods in the following paragraphs along with formulas and examples.
How to find the area of a Triangle?
1) Area of the triangle when the length of the base and the height is given:
If we know the length of the base (or its longest side) of a triangle and its perpendicular distance from the opposite vertex (its height), we can use the formula:
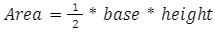
to calculate its area.
Example:
A triangle ABC has sides of lengths 3 cm, 5 cm and 7 cm. The height of the vertex opposite the longest side is 2 cm. Find the area of the triangle?
Soln:
We have been given the lengths of the three sides of the triangle ABC and the height of the vertex opposite the longest side. Thus, we can apply the formula for the area of a triangle in this case to calculate the area.
The length of the longest side =7 cm
Height of the vertex from the longest side = 2 cm
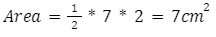
2) Area of a triangle when the length of two sides and angle contained by them is given:
If we are given the length of two sides of the triangle and the angle contained by them, the area can be calculated by using the formula:
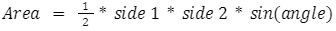
Example :
ABC is a right-angled triangle which is right-angled at A. AB=3 cm and AC=4cm, then find the area of the triangle ABC.
Soln:
Given that the triangle ABC is right-angled at A, the value of angle A=90 degrees. We are also given the length of two sides containing angle A, which would allow us to use the formula
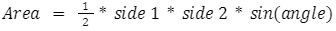
to find the area of the triangle very easily.
AB= 3 cm
AC= 4 cm
Angle A= 90
Sin A =1
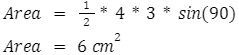
Therefore the area of the given triangle is equal to 6 cm sq units.
NOTE:
The given triangle is right-angled at A, so we can also use the Pythagoras theorem to find the length of the side BC.
By Pythagoras theorem, we know that:
BC2=AC2+AB2
BC2=32+42
BC2=9+16=25
BC=5 cm
Thus BC is a side of length 5 cm
3) Area of a triangle using Heron’s formula:
There are times when we are given only the lengths of the three sides of a triangle. Using Heron’s formula, we can also calculate the area of a triangle in this case. Heron’s formula first requires us to calculate a value known as semiperimeter and then plug it into the formula. As the name suggests, the semi perimeter is half of the perimeter of the triangle.
Here,
P=a+b+c
Let, S=P/2.
Area in Heron’s formula is given by:
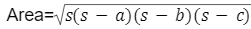
where s denotes the semi perimeter of the triangle, and a,b,c represents the length of the sides of the triangle.
Example:
A triangle ABC has sides in the ratio of 3:4:5, and its perimeter is equal to 36 cm. Find the area of the triangle.
Soln:
Let the sides of the triangle be 3x,4x and 5x, respectively.
Perimeter =3x+4x+5x
36=3x+4x+5x
36=12x
3=x
So the lengths of the sides of the triangle are 9 cm, 12 cm and 15 cm, respectively.
Given that the perimeter is 36 cm:
The semi perimeter of the triangle equals 36/2=18 cm
This can also be verified by using the formula for semiperimeter which is (a+b+c)/3.
After we have obtained the semi perimeter, we can use Heron’s formula directly to calculate the area of the triangle.
Thus the area of the given triangle is equal to 54 cm squared units.
Conclusion
A triangle is a closed geometrical figure with three sides whose interior angles sum up to180 degrees. The area of a triangle can be calculated in many ways. Some methods of calculating the area of a triangle are by using the basic formulas or by using Heron’s formula. The calculation for the area of a triangle is required in many scientific calculations. The most important thing to remember while calculating the area of a triangle is to get the necessary data from the problem and avoid making any arithmetic or calculation errors.
