Watch Free Classes

A circle is a shape with a smooth curve, no angles, and no starting and endpoints. A circle is a closed figure without any sharp edges or vertex. In other words, it can be said it is a closed, smooth, and looped figure without edges. A circle has two dimensions. 

Some examples of a circle are the wheel, bottle mouth, circular object’s base, etc. The area of a circle is easy to calculate and can be calculated using a single formula.

But, before that, there are many more things to know about this topic. So, let’s move forward to some of the important terms related to the circle’s area.

Some Important Terms

  1. Circle: A closed, smooth, and looped figure without edges is called a circle. A circle has two dimensions.
  2. Closed Loop: A closed-loop is a curved figure that does not have any edges, and its starting and endpoints are the same.
  3. Radius: The measurement of a straight line that originates from the centre of a circle and goes to its circumference is called a radius.
  4. Diameter: A straight line through the centre of a circle which cuts the circumference two times is called the diameter.
  5. Area: It is the total region on the inside of any figure.

Area of A Circle and Its Applications

The area of a circle is defined as the area or region covered or occupied by the circle. The SI unit of the area of the circle is m2, and the CGS unit is cm2. The area of the circle has a major role in mathematics and is used across various industrial sectors. 

Some applications for the area of the circle are listed below:

  • It is used by architects to design buildings and by civil engineers for construction-related tasks
  • It is used by engineers in designing vehicles like aeroplanes, rockets, spacecraft, etc
  • It is used by clockmakers to set and synchronise the hands of the hour, minute, and second hands
  • It is used in making dome-like structures in buildings
  • It is used by space agencies and astronomers to calculate the path of planets and satellites

Formulas of Area of Circle

The formula used for calculating the area of a circle is:

Area of Circle=πr2

,here,  r = radius of the circle.

This is the radius formula. If the radius is given, the area of a circle can be simply calculated by putting the value of radius in the formula and the value of pie, which is 22/7. But if the diameter of the circle is given, not the radius. Then, the following formula can be used:

ss1

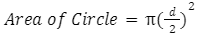
,here,   d = diameter of the circle.

In this formula, the diameter of the circle is taken into use, not the radius of the circle. As the diameter is two times the radius. Therefore, the diameter is halved and then squared to get an equal magnitude. There is one more formula for calculating the area of a circle if the diameter of the circle is given, which is:

ss2

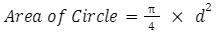
This formula also gives the same value for the area of the circle as the above; both will give. These are the formulas when the radius or diameter of the circle is given, but what if both are not given. So, let’s take a look at the formula that uses the circumference of the circle. The formula is given below:

ss3

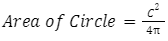
Here,

C = circumference of the circle.

In this formula, the circumference is used to calculate the area. Here, the circumference of the circle is squared and then divided by four times the pie.

Guide on Calculation of Area and Examples

The calculation of the area of the circle is very simple. The only thing to be kept in mind is whether the radius, diameter, or circumference is given, and apply the relevant formula.

To develop a better understanding of the topic, let’s take a look at some of the questions related to the calculation of the area of the circle.

Q1. The radius of a circle is 7 cm, then find its area.

Given,

r = 7 cm

Since,

ss4

Q.2 The circumference of a circle is 4 cm, then find its area.

Given,

C = 4 cm

Since,

ss5

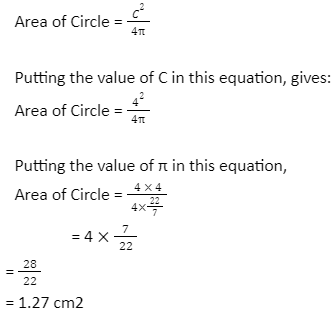
Conclusion

The calculation of the area of a circle can be done in many ways and formulas. The only thing that should be kept in mind is what is given in the question and apply the formula accordingly. As we discussed above, there are several formulas, one for radius, one for diameter, and one for circumference.

The area of the circle has many important applications in various professional fields, especially in engineering models, construction, and many more.