In mathematics, a factorial is the product of all non-negative integers that are less than or equal to a non-negative integer (n) that is given. The symbol n (positive integer) is ended with the symbol of factorial – an exclamation (!). The fundamental representation of factorial is n! = n (n-1)(n-2)……2(1). Here, n! represents the multiplicative product of all the non-negative integers lower than or equal to the integer n. The factorial was first defined by an author from Britain named Fabia Stedman in 1677. He defined a factorial as an equivalent to change ringing. Change ringing is a sequence in a musical performance that involves ringing multiple tuned bells. Later, in 1808, a French mathematician established a symbol for factorials – n!. In mathematics, factorial is important in various areas like probability, graph theory, statistics, algebra, number theory, and many more.
What is factorial?
This section will address the question – what is factorial?
The factorial of a number (n) is defined as a function that multiplies all the non-negative numbers less than n.
Representation for n factorial – n!=(n-1)(n-2)……..(2)(1).
Here, n is a positive integer.
Let us look at an example – 5! =5 4 3 2 1 = 120
What is zero factorial?
The factorial of zero is equivalent to 1. It is represented as 0! = 1
For n = 0, n! involves products of no numbers. Hence, this is an example of an empty product (no factors for a product) equivalent to the multiplicative identity in broader terms.
The zero factorial definition involves only a single permutation of zero (no objects). This definition also justifies various identities in combinatorics.
Terms to be familiar with when defining zero factorial.
- Combinatorics – this field of mathematics majorly focuses on counting
- Permutation refers to the arrangement of objects of a set into a sequence
Factorial of negative numbers
This section will see if we can have factorial values for negative numbers like -2, -4, etc.
Let us start from 4 factorial and go downwards until we reach a negative value of -1.4! = 4 3 2 1 = 24.
3! =4!/4 =6.
2! = 3!/3 =2.
1! =2!/2.
0! = 1!/ 1 = 1.
-1! = 0!/0 = 1/0.
The value for the negative number -1 is undefined, as 1 cannot be divided by zero. From this, we can conclude that factorial of negative numbers is not possible.
Uses of factorial
Permutations
One of the primary uses of factorial is the area of permutation. There are n! Variety of ways of arranging n distinct items. The formula for permutation is
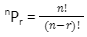
where P denoted the number of permutations, n denoted the total items in a set, and r is the number of items selected from a set .
Combinations
Factorials are used in combination problems. Combinations are where the grouping outcomes do not depend on the order. The formula is
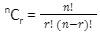
- Factorials are used in the binomial theorem in algebra. The binomial theorem uses factorials to expand the power of sums
- Notably, factorials are in the denominator of Taylor’s formula in the area of calculus
- Factorials appear in the denominator of the power series. The exponential series is the most notable in which factorials are used
- In probability theory, factorials are highly used in the Poisson distribution
- Legendre’s formula in number theory elucidated the property of factorials to divide n! all non-negative integers up to n
- Factorials are not only limited to the field of mathematics. They appear in quantum and statistical physics formulae
Similar Sequences to Factorial
This section will highlight a few sequences that are similar to the factorials.
- Multi-factorials – this type of factorial uses multiple factorial symbols (multiple exclamation marks)
- Double factorials (n!!) – is a type of multi-factorial. These factorials are used to make trigonometric integrals simpler
- Primorials – help get prime number products that are less than or equal to n
- Super-factorials – this factorial is a consequence of multiplying the first n numbers. The Barnes G-function continuously interpolates this function
- Hyper-factorials – are a consequence of multiplying a number multiple times between the range of 1 to n
Solved Problems for Factorials
1. Calculate the factorial of 7 –
7! = 7 6 5 4 3 2 1 = 5040.
2. Factorial used in permutation problem –
A group of 10 received 200, 300, and 50 rupees cash prizes. Calculate how many ways the rewards can be distributed?
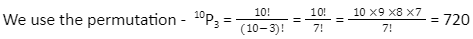
Hence, the prizes can be distributed in 720 ways.
Conclusion
This article focuses on what is factorial. The factorial of a number (n) is defined as a function that multiplies all the non-negative numbers less than n. Factorials are extensively used in mathematics like probability, graph theory, statistics, algebra, number theory, and many more. The factorial of zero is equivalent to 1. It is represented as 0! = 1. Factorial values of negative numbers are not defined. Factorials are used in many mathematics topics like permutations, combinations, binomial theorem, Taylor series, Poisson distribution, and many more. It is not restricted to mathematics applications but is also applicable in quantum and statistical physics. The sequences that are analogous to factorials are super factorials, multi-factorials, double factorials, primorials, and hyper factorials.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






