Differences Between Regular and Irregular Polygons

A regular polygon has equal angles and sides, meaning that all sides are the same length. On the other hand, an irregular polygon has sides of varying sizes and varying angles. Therefore, when deciding between regular and irregular polygons, it’s crucial to consider the sides and angles of the shapes.

You will learn about equilateral and isosceles triangles, for example. 

• By definition, an equilateral triangle has all sides of equal length and angles, making it a regular polygon. 
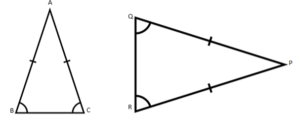
• The sides of an isosceles triangle aren’t all the same length, and the angles are also different, as shown in the illustration below.

Regular Polygon

A regular polygon is a two-dimensional figure with equal-length sides and equal-measured interior angles. A regular polygon can be both convex and concave.

The most frequent regular polygons and their distinguishing characteristics are below.

Formulas

Interior Angle

Interior angles appear inside the polygon at its corners when the line segments unite end-to-end. We’ll look at how to get the total of the internal angles in any n-sided regular polygon and how to calculate the individual angles.

Sum of Interior Angles

It’s the total of all the polygon’s internal angles added together. We partition a regular polygon into triangles to find the sum of the internal angles. Because the total of all the internal angles in a triangle equals 180 degrees, multiplying the number of triangles in the polygon by 180 degrees yields the sum of interior angles in a regular polygon.

One Interior Angle

Because all the sides of a regular polygon are equal, knowing the total of all the interior angles allows us to quickly compute the measure of any angle by dividing the sum by the number of sides in the polygon.

Irregular Polygon

An irregular polygon, also known as a non-regular polygon, is a form that does not have all of its sides and angles equal in length. 

Examples of Regular and Irregular Polygons

Irregular polygons include the scalene triangle, rectangle, trapezoid, and kite. Pentagons and hexagons can be irregular polygons if their sides and angles are not equal.

Regular and Irregular Polygons and their Properties

Regular Polygon Properties

• The rotational symmetry of order n exists in a regular n-sided polygon
• A regular polygon’s vertices are all concyclic points since they all sit on a circle (the circumscribed circle). A regular polygon is a cyclic polygon, in other words
• Including the characteristic of equal-length sides, every regular polygon has an inscribed circle or incircle at the midpoint that is tangent to every side. As a result, a tangential polygon is a regular polygon
• If and only if the odd prime elements of n are distinct Fermat primes, we can form a regular n-sided polygon with compass and straightedge
• All perpendiculars drawn from the centre to the sides of a regular polygon are equal

Irregular Polygon Properties

These polygons have a few distinguishing features that distinguish them from other polygons. The following are the properties:

• Irregular polygons have endlessly huge sides because their lengths are not equal
• There are many ways to shape irregular polygons, both fundamental and advanced
• Parallelograms, trapeziums, and quadrilaterals are irregular polygons since their adjacent sides and angles are not equal

What is the Difference Between Regular and Irregular Polygons?

After knowing what regular and irregular polygons are, you should understand the differences.

• In many cases, the terms might also provide some clues. A right-angled triangle, for example, has a right angle, which means it can’t be a standard form (the angles of an equilateral triangle are all 60 degrees). As a result, it’s an outlier
• Examine the sides and angles once you’ve visualised it or if you have an image. Of course, if you recall the shape’s attributes (a rectangle, for example, has equal angles, but not all sides are identical), you’ll know the solution. Looking at the sides and angles can help if you’re not sure
• First, ask yourself this question: are all of the sides equal? Even though the polygon has two equal sides, if the others are of varying lengths, it’s an irregular shape, and you’ve found your answer! However, if all sides appear equal, look at the angles
• Does it appear that the angles are equal? If they are, and you’ve double-checked the sides, it’s a regular shape. It’s an irregular polygon if the angles are different

Conclusion

Polygons are two-dimensional closed figures of three or more line segments joined together. Regular and irregular polygons are the two forms of polygons. A regular form is one in which all sides are equal, and all interior angles are equal. There are no equal sides or angles on an irregular shape. These two shapes are considered irregular polygons when the angles and sides of a pentagon and hexagon are not equal.