Profile
Settings
Refer your friends
Sign out
The counting of the cube is nonverbal reasoning; the learner has to count the numbers of the cube from the given figure. They have to understand the pattern of the cube that is structured in the model; it can help them to count the number of cubes present in the structure. The counting of the cubes required the basic knowledge from the learner that they knew the faces of the cube.
Discussion
Measurements help to determine the size and the volume of the solid particle. In measuring the volume of the model, the number of small cubes should be counted to find the volume of the model. The volume can be explained as the space taken by the model. The question on the counting of the cube in the given model is the type of non-verbal reasoning. The solving of these types of problems improves the thinking power of the mind. The different patterns are created from the small cube however they are two famous patterns that are Vyshan and Hema patterns. Another famous pattern that can be easily seen in daily life is the Rubik cube.
In the counting of cubes in the given figure, the learner should have a clear concept of the basic theory of the cube and dice such as the number of faces present in the cube, the vertices present in the cube. A cube is a three-dimensional structure of the square that consists of twelve vertices, six faces, and eight vertices. In daily life, a Rubik cube can be easily seen as an example of a cube. A Rubik cube contains nine small structures of cube that are arranged in a pattern to make a big cube. The use of the Rubik cube does develop the mind of the person. The counting of the cube with the figure is asked in the competitive exam. The learner has to count the numbers of the small pieces of the cube present in the given figure.
All the dice are cubes, they have six faces, and all the angles inside the cube are 90 degrees. All sides of the cube are equal to each other. The rules that are used to count the numbers of the cubes in the given structure can be also used in the counting of the dice; both the dice and cube follow similar rules.
There are two different types of patterns to count the number of the cube in the given figure.
- Vyshan’s pattern
- Hema’s pattern
The Vyshan pattern is further divided into three patterns, in the first pattern 7 cubes are counted and that is the smallest number of cubes required to make the Vyshan pattern. In the second pattern, 32 cubes are required and in the third pattern, 81 cubes are required. The second pattern is the Hema pattern; in the first pattern 20 cubes are required to make the pattern of Hema. In the second pattern of Hema 32 cubes are required, and in the third pattern, 44 cubes are required. The total number of the cube in the pattern can be explained as (n+2) power 3, n is the number of the cube. The formula to make the Hema pattern from the cube is 12n + 8 and the formula to make the Vyshans pattern is (n + 2) power three minus (12n + 8). These are the patterns that are used to make a figure from the small cubes and dice to make a big structure. The inner side of the vyshan pattern is solid and it is full with a small cube inside the structure while in the Hema pattern the inner structure is not filled with the cube. The inner part of the Hema pattern is empty however the side of the pattern is full with the cube. The structure from the vyshan and Hema can be mixed to make a big and perfect cube.
Count the number of cubes in the given figure:
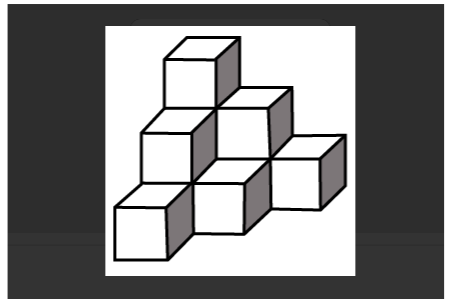
In the above figure, it is clearly mentioned that there are I columns that contain 2 cubes, 2 columns contain 2 cubes each and 3 columns contain 1 cube each.
Number of cubes in column of 3 cubes= 1*3=3;
Number of cubes in column of 2 cubes=2*2=4;
Number of cubes in column of 1 cubes=3*1=3;
Therefore total number of cubes= 3+4+3=10
Hence the number of cubes is 10 in the above given figure.
Conclusion
In the assignment of counting the numbers of the cube, the learner can use the different patterns in the model to count the numbers of cubes present in the cube. The cube has six faces and eight vertices. Two patterns are discussed in the assignment. The pattern is based on the structure that has been made from the small cubes. The different patterns discussed in the assignment require different numbers of the cube to make a structure based on that pattern. The Vyshan pattern requires more numbers of the cube to make the model based on the Vyshan pattern.
