Geometry is a field of study that deals with the structure of individual objects, their spatial relationships, and the characteristics of the environment. Euclidean Geometry, Differential Geometry, Non-Euclidean Geometry, Projective Geometry, Analytic Geometry, Topology, and others are some branches of geometry.
Many different geometry formulae are divided into one dimensional, two dimensional, and three dimensional.
Basic Geometry Overview
Geometry is one of the eldest mathematics disciplines, with an extended application history. It has a wide range of practical uses. The forms, sizes, and placements of objects, for instance, planets, stars, and the moon have always interested mathematicians, without actually estimating it by going there, which was physically impossible. Geometer is the name of the person who studies “Geometer”.
Major or Significant Branches of Geometry
There are numerous branches of geometry, depending on the applications.
Some of the significant branches of geometry are as follows.
- Analytic Geometry: This geometry represents algebraic equations and was introduced by the French mathematician René Descartes (1596–1650). This French mathematician was the first to use rectangular coordinates to find points and to use algebraic equations to draw lines and curves.
- Euclidean geometry: A kind of geometry suited to the connections between the lengths, the areas, and the volumes of physical figures established in ancient societies. This geometry acquired prominence after being formalised in Euclid’s elements, which were based on ten axioms, or postulates, from which deductive logic established a hundred theorems.
- Differential Geometry: A German mathematician proposed the field that deals with differential geometry following practical surveying and geodesy concerns. The innate characteristics of the curves and the surfaces are differentiated using differential calculus. For example, he defined the cylinder’s intrinsic curvature as comparable to that of a plane, as demonstrated by cutting the cylinder through its axis and compressing it, but not as being similar to a sphere, which cannot be compressed further without distortion.
- Non-Euclidean Geometry: Several mathematicians devised substitutes for Euclid’s concurrent postulate, which states, “Provided a line and a point not present on the line, it is possible to form precisely one line that is parallel to the line along with the given point.” A Sphere is an example of non-Euclidean geometry.
- Projective Geometry: Projective geometry was created by the French mathematician Sir Girard Desargues (1591–1661) to deal with the properties of geometric objects that cannot be altered by projecting their image, or “shadow,” onto another surface.
- Topology: Topology, the newest and most inventive field of geometry, focuses on the attributes of geometric forms that do not vary when they are elongated, compressed, or pleated but not ripped.
Some fundamental figures and geometrical formulas related to it
1. 2D Figures:
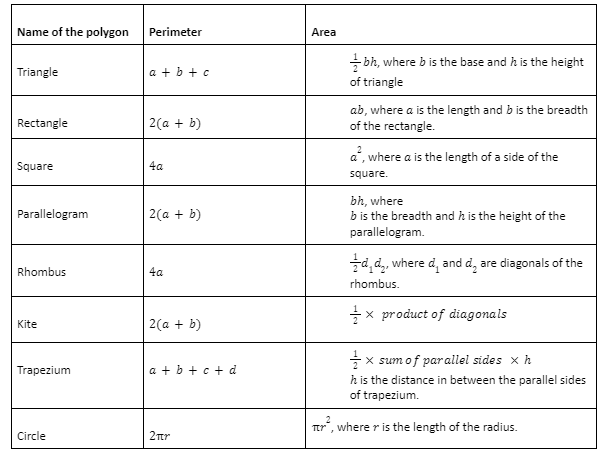
2. 3D Figures:
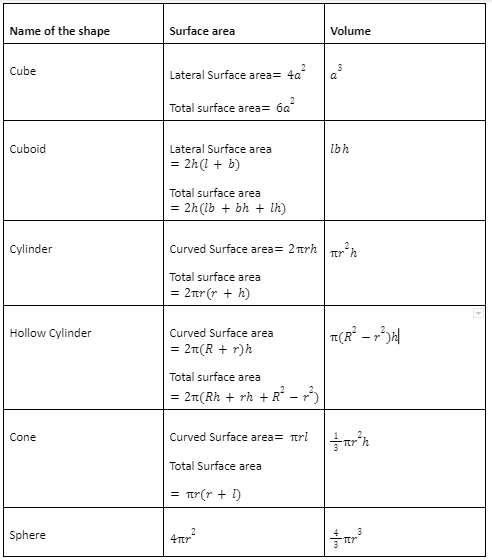
Conclusion
Geometry is a mathematical concept associated with the structure of items, their spatial relationships, and the qualities of the environment. It’s one of the ancient fields of mathematics, having evolved in response to practical matters like those encountered in surveying. Its name is taken from Greek words that mean “measuring of the Earth.”
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






