HCF is an abbreviated form of highest common factor, and LCM is the abbreviated form of lowest common multiple. The definition of HCF and LCM is simple. The HCF of two or more numbers is the most significant number that divides them entirely. The LCM of those numbers is the least number that can be exactly divisible by two or more given numbers. There are different formulas and methods for finding HCF and LCM of two or more numbers, such as the division or prime factorisation methods. The HCF and LCM are also related in some ways.
Definition of HCF and LCM
- HCF – The HCF of two or more numbers is the most significant number that divides them entirely. For instance, the HCF of 12 and 16 is 4
- LCM – The least number which can be exactly divisible by two or more given numbers is known as LCM of those numbers. For instance, the LCM of 12 and 16 is 48
Factor
To understand what is a factor, let’s look at an example:
Let’s take two numbers, 15 and 12.
Now 15x 1= 15
3x 5= 15 and 5×3 = 15
Therefore factors of 15 are 1, 3, 5, and 15.
Similarly 12x 1= 12
2x 6 = 12
3x 4= 12
So factors of 1 are 1, 2, 6, 3, 4 and 12.
Finding HCF
We can consider two methods to find the two numbers’ highest common factor ( HCF). These two methods are the prime factorization method and the division method.
Division Method
There are three steps in finding the HCF by the division method. The steps are as follows:
- Step 1- Division of larger numbers by smaller numbers.
- Step 2- A remainder will be obtained from Step 1. Consider this remainder as the divisor, and the last divisor is taken as the dividend.
- Step 3- The second step should be repeated until 0 is obtained in the remainder. The last divisor which is obtained will be the HCF.
Let us take an example. Let’s find out the HCF of 28 and 84.
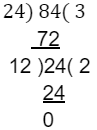
Hence, the HCF of 24 and 84 is 12.
Here, we followed the three steps mentioned above.
Prime Factorisation Method
In this method, each given number must be expressed as the product of prime factors. The product of the least common prime factor will give the HCF of those numbers.
We take the following steps to find the HCF of 24 and 84 by this method.
24= 2x2x2x3
84=2x2x3x7
To find the HCF, we multiply such prime factors, which are common in both the numbers.
HCF= 2x2x3= 12.
How to find the LCM of two Numbers?
Like the HCF, we can find the LCM of two numbers by the methods of prime factorization and division.
Prime Factorisation Method
There are two steps in this method.
- Step 1 – Express each number as a product of its prime factors.
- Step 2 – Determine the product of those prime factors that appear the most times in the prime factorization. The product is the required LCM.
Let’s understand this by taking an example. Find the LCM of 72 and 240.
72= 2x2x2x3x3
240= 2x2x2x2x3x5
Hence LCM= 2x2x2x2x3x3x5= 720.
Division Method
We follow the same steps as we did in finding HCF to find LCM by this method. The only difference is that we will multiply all the numbers obtained in the end in the last step instead of multiplying the common factors.
HCF and LCM Formula
The formula of HCF and LCM is
Product of two numbers= LCM of two numbers x HCF of two numbers.
The following formulas can be deduced from the HCF and LCM Formula.
HCF of two numbers= Product of two numbers/ LCM of two numbers.
LCM of two numbers= Product of two numbers/ HCF of two numbers
Let us consider an example. Let X and Y be two numbers, then.
Product of X and Y= HCF of X and Y x LCM of X and Y
Some points about HCF and LCM
- LCM of two numbers is never less than the two given numbers.
- The HCF of two numbers is never more than the allotted two numbers.
- For two or more prime numbers, the HCF is 1
- For two prime numbers, the LCM is equal to their products.
- The HCF and LCM are related by HCF and LCM formula.
Product of two numbers= LCM of two numbers x HCF of two numbers.
Conclusion
The complete form of HCF is highest common factor, and that of LCM is the lowest common factor. The HCF of two or more numbers is the greatest number that divides each of them fully. The LCM of those numbers is the least number that can be exactly divisible by two or more given numbers. The HCF and LCM are related by the HCF and LCM formula. We can find the HCF and LCM by the prime factorization and division methods. The HCF of two numbers is never more than the given two numbers, whereas the LCM of two numbers is less than the two given numbers.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






