The concept of permutation and combination was developed in the 17th century. Permutation and combination are the tools used to arrange or rearrange a collection or set of data in a specific manner. It makes it easier to calculate the biggest of the biggest probabilities and many other things. There are formulas to calculate the permutation and combination, and we will look at them.
But, before that, there are many more things to know about this topic. So, let’s move forward and look at some of the essential terms related to permutation and combination.
Some Important Terms
- Permutation: The selection of data or objects from a certain group of sets or forming subsets is known as permutation.
- Combination: The order of representation of data or objects in a certain group is called combination.
- Sets: When a well-defined element or object is collected together, it is known as a set.
- Factorial: It is denoted by an integral value followed by an exclamation mark. Basically, it is the product or multiplication of the given positive integer, followed by the positive numbers less than it.
Permutation and its Uses
A permutation is a vital tool of mathematics used when the sequence or order of an arrangement is needed. The use of permutation is in almost every field as well as mathematics. In computer science, it is used for analysing sorting algorithms. In quantum physics, it is used to describe the states of particles. In biology, it is used in the description of RNA sequences.
It also has many real-world uses, which are listed below:
- Forming word anagrams
- Protein formation in the body
- Working out the ways to win a lottery
- Several seating arrangements
- Cracking codes
- Finding out the numbers of available phone numbers
- Making phone numbers
- Making car plate numbers
- Order in which contestants finish a race
Formula and Calculation of Permutation
The formula for permutation, which is used to calculate the permutation, is given below:
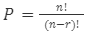
Where
‘n’ is the item present in the set.
‘r’ is the number of items taken for the permutation.
‘!’ is the exclamation mark that denotes factorial.
It can be calculated simply by putting the values of these variables into the formula. Generally, the expression of this formula is to find the number of arrangements or number of ways in which ‘r’ can be arranged from a set of ‘n’ if the order matters. Look at the question below, which will describe the formula very well.
Q. How many arrangements of seating can there be if 10 people want to sit and there are 10 seats?
Here, the required set has 10 items, as there are 10 seats.
Therefore, n = 10
The items taken for permutation are also 10, as there are 10 persons.
Therefore r = 10
Putting these values in the formula,
P = n!/(n-r)!
P = 10!/(10-10)!
P = 10!
P = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
P = 3628800
Hence, there are 3628800 arrangements possible to seat 10 persons on 10 seats.
Combination and its Uses
The combination is a mathematical technique or tool that determines all the possible ways to group a certain data that arranges a collection of data in all possible groups. In combination, the items can be selected in any order; in this, the order of arrangement does not matter, unlike in permutation.
It also has many real-world uses, which are listed below:
- Making lottery numbers
- Selecting nominees for student council
- Selection of menu
- Selection of food
- Selection of clothes
- Selection of subjects
- Selection of the team
Formula and Calculation of Combination
The formula for combination is:
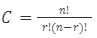
Where,
n = Total items in the set
r = Items taken for the permutation
“!” denotes factorial
It can be calculated simply by putting the values of these variables into the formula. Generally, this expression of this formula is to find the number of possible arrangements or number of ways in which ‘r’ can be arranged from a set of ‘n’ if the order doesn’t matter. Let’s understand it by an example.
Q. There are 10 balls in a box. What is the number of ways of picking 8 balls from it?
Here, the required set has 10 items, as there are 10 balls in the box.
Therefore, n = 10
The items taken for combination are 8, as it is required to pick 8 balls from it.
Therefore r = 8
Putting these values in the formula,
C = n!/r!(n-r)!
C = 10!/8!(10-8)!
C = 10!/8! x 2!
C = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 / 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 x 2 x 1
C = 3628800 / 40320 x 2
C = 3628800 / 80640
C = 45
Hence, there are 45 ways to pick that 8 balls from the box of 10 balls.
Conclusion
As we have discussed above, permutation and combination are the two most essential tools of mathematics that are used to arrange or rearrange a certain set or collection of data in a specific or patterned manner and to find the total number of possible ways or arrangements of arranging a specific group or collection of data, respectively. There are formulas for both, which are discussed already. They are instrumental in day-to-day life, as it makes the calculations very easy that seem impossible. Not only in mathematics, but they are also used in almost every other sector.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






