Profile
Settings
Refer your friends
Sign out
Train problem is a quantitative aptitude problem related to speed, time, and distance.
Major Concepts of Problems on Trains
The concepts of train problem can be divided into four parts:
- Conversion
- Time and Distance formula
- Train and Object
- Theory of Relativity
Conversion
The questions ask to convert the speed of the train from,
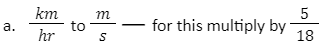
We do this because 1 km = 1000 m and 1 hr = 3600 seconds.
Which means conversion, in this case, should be 1000/3600 = 5/18, when simplified.
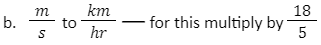
Tricks and Tips
- We may get confused about what to multiply for a given question. While knowing where the numbers come from helps, we have some other tips to remember
- To simplify, remember: when converting to smaller (km → m), the numerator should be smaller than the denominator. Hence, 5/18
- Similarly, when converting to bigger (m → km), the denominator should be smaller than the numerator. Hence, 18/5
Example 1: Convert 24km/h to m/s.
Soln:
We know that
Hence, we get 24x(5/18)=6.66m/s.
Time and Distance Formula
This type of problem is based on the concept of speed. Speed is defined as distance travelled per unit of time.
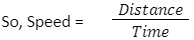
Tricks and Tips:
- Write down the data which is available
- Remember the formula that Speed = Distance/Time
- Any two out of the three will be given. We will be required to find the third measure
- It is important to know the units of all three
- Ensure that all the units are the same while calculating. For example: if speed is given in m/s and distance in km, it is important to convert the distance into m
Example 2: A train is travelling 200 m and runs at a speed of 50 m/s. How much time will be required to cover the distance?
Soln:
With the given available date we can say that,
- Speed = 50 m/s
- Distance = 200 m
We know the formula that,
Speed = Distance/Time
Therefore, 50 = 200/t
t = 200/50 = 4 s
Hence, the train will cover the given distance in 4 seconds.
Train and Object
This subsection consists of two cases.
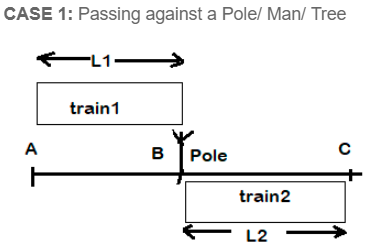
- The train will pass the pole completely when the back of train 1 will come at point C
- The required formula is
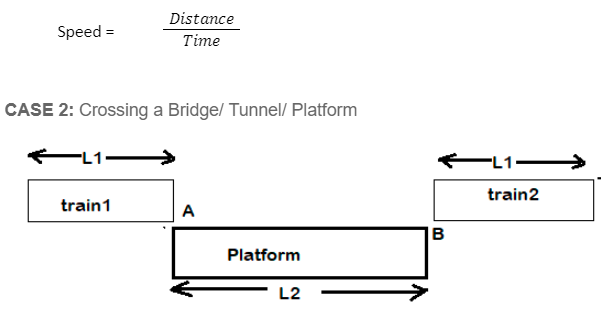
- When the back end of the train passes point B, the train will have completely crossed the platform
So, the distance travelled by the train is L1 + L2. .The formula, then, is:
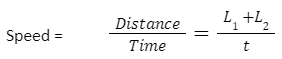
Example 3: A train is 300 m long and is running at a speed of 54km/hr. How much time does it take to pass a bridge, which is 100 m long?
Soln:
We first write the given data,
- Train length = L1 = 300 m
- Bridge length = L2 = 100 m
- Speed = S = 54 km/hr
Converting 54 x (5/18)= 15 m/s
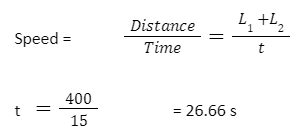
Hence, the time required to pass the bridge is 26.66 seconds.
Example 4: A train covers a distance of 10 km in 10 minutes. If it takes 6 seconds to pass a telegraph pole, then what is the length of the train?
Soln:
We are given that the train covers 10 km distance in 10 minutes.
Speed = Distance/Time
Converting 10 min = 10 x 60 = 600 s
Now, distance = 10 x 1000 = 10,000 m
Applying the above formula we get
Speed = 10,000/600 = 16.66 m/s
Now, it is given that it takes 6 s. To pass the pole,
Distance = Speed x time
Distance = 16.66 x 6 = 99.96 m
Hence, 99.96 (approximately 100 m) is the length of the train.
Theory of Relativity
This subsection has the following two cases.
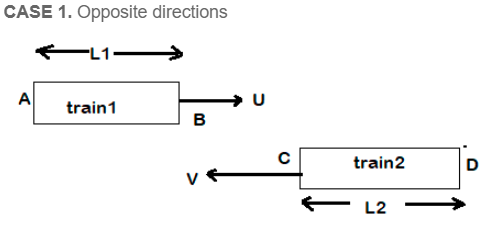
- In this, we say that the trains have crossed each other completely, when if B and D cross each other.
- So, the lengths L1 and L2 have to be covered.
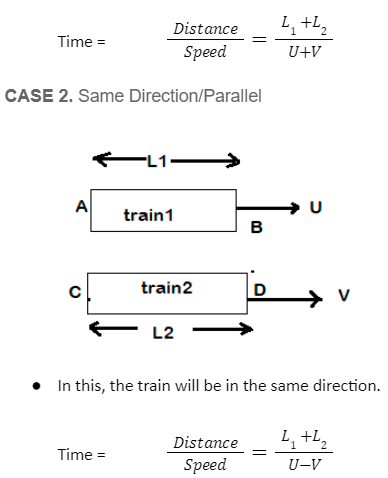
Example 5: If two trains, 100 m and 200 m long, at speeds of 600 km/h and 30 km/hr, are running in opposite direction, what is the time taken by trains to cross each other?
Soln:
We know that:
Length of train1 = L1 = 100 m
Length of train2 = L2 = 200 m
Speed of train1 = U = 60 km/hr
Speed of train1 = V = 30 km/hr
As they are in opposite directions,
S = U + V = 90 km/hr
Convert 90 km/hr into m/s = 25 m/s
Now, using the formula of CASE 1
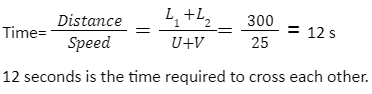
Example 6: Two trains of equal length are running parallel in the same direction. Their speeds are 40 km/hr and 30 km/hr. The faster train passes the slower train in 30 seconds. What are their lengths?
Soln:
We know that as they are in the same direction. Hence, we apply CASE 2.
U = 40 km/hr and V = 30 km/hr
U – V = 10 km/hr
Converting 10 km/hr = 2.77 m/s
As lengths are equal L1 = L2 = L.
Hence, applying the formula:
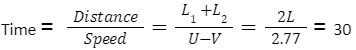
2L = 30 x 2.77
L = (30 x 2.77)/2
L = 41.66 m
Hence, the length of the trains is 41.6 m.
Conclusion
- From conversion from km/hr to m/s, multiply it by 5/18.
- Conversion of m/s to km/hr, multiply by 18/5.
- The general formula for speed is given as Speed = Distance/ Time.
- The train appears to move faster when in the opposite direction then to when in the same direction. This is known as the theory of relativity.
- When the trains are moving in different directions, we add the speed of the trains. When in the same direction, we subtract it.
