State and Prove Bernoulli’s Theorem

Answer:

A Swiss mathematician Daniel Bernoulli (1738) discovered this theorem that describes the total mechanical energy of the moving fluid, consisting of the energy associated with the fluid pressure and gravitational potential energy of elevation and the kinetic energy of the fluid remains constant. 

Bernoulli’s theorem states the principle of conservation of energy for standard fluids. This theorem is the basis for many engineering applications.

Proof

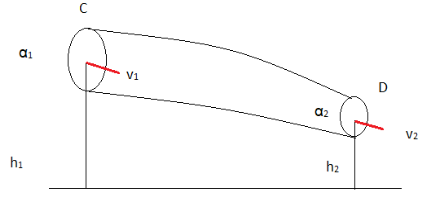
Let’s consider a tube of flow CD as shown in figure A. Let, at point C, α₁ be the cross-sectional area, v₁ be the velocity of the liquid and P₁ be the pressure. On the other hand, let α₂ be the pressure, v₂ be the velocity and P₂ be the pressure at the point D. Let, h₁ and h₂ be the heights of the tube by which the tube is raised.

Figure A

The force exerted by the liquid at C is P₁α₁.

The work done by the mass entering the tube through the cross-sectional area α₁ at the point C per unit time is P₁V.

Where, 

 V= α₁v₁ is the volume of the liquid entering C.

The work done is stored in liquid and is called pressure energy.

So, the pressure energy per unit volume at the end C is P₁.

If m is the mass of the liquid entering at the point C per unit time, then the pressure energy of the liquid at C= m (P₁/ρ).

where pressure energy per unit mass is P₁/ρ 

and ρ is the density of the liquid.

The kinetic energy of the liquid at the point C is ½ mv₁²

The potential energy of the liquid at the point C is mgh₁

So, the total energy at the point C is given by,

mP₁/ρ + ½ mv₁² + mgh₁                           (1)

Similarly, the total energy at the point D is given by,

mP₂/ρ + ½ mv₂² + mgh₂                           (2)

From the principle of conservation of energy,

m P₁/ρ + ½ mv₁² + mgh₁ = mP₂/ρ + ½ mv₂² + mgh₂

or, P₁/ρ + 1/2 v₁² + gh₁ = P₂/ρ + 1/2 v₂² + gh₂

or, P/ρ + ½ v²+ gh = constant

This is Bernoulli’s theorem.

P/ρg+ v²/2g+ h = constant

P/ρg is called the pressure head

v²/2g is called the velocity head

h is called elevation head.