Write the Smallest 5-digit Number and Express it in the form of its Prime Factors by Tree Diagram.

Q. Write the smallest 5-digit number and express it in the form of its prime factors by tree diagram.

Answer: Now, if you have to think of a number that is the smallest, which digit comes to your mind? Probably 0 or negative. But any number cannot be started with a negative digit or 0. And hence, the smallest first digit of a number is 1.

And since we have to find a smallest 5-digit number, 1 would be followed by the smallest numbers subsequently i.e. 0

As a result, the smallest five digit number will be 10000, where 1 would be in ten-thousandths place followed by 0 to complete a number.

Let’s understand its prime factorization. The numbers having two factors, 1 and the number itself, are known as prime numbers, for example, 2, 3, 5, 7, 11, 13, 17, 19 and so on.  Therefore, a method of representing a number as a product of its prime numbers is known as prime factorization. To understand this concept, let’s take 30 as a number and find its prime components.

30 = 5×6, whereas 6 is not a prime number, it would be further break into prime numbers –

30 = 5 × 2 × 3

Now, the prime factors of 10,000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5

To find the prime factors of a number, one case use Tree Method –

The factor tree approach involves finding a number’s factors and then factorising those numbers until we reach prime numbers. Placing the number at the top of the factor tree is a good idea. Then, as the tree’s branches, write down the relevant pair of factors. Factorise the composite factors discovered and write the pair of factors as the tree’s next branches. Repeat this process until all of the composite factors’ prime factors are found.

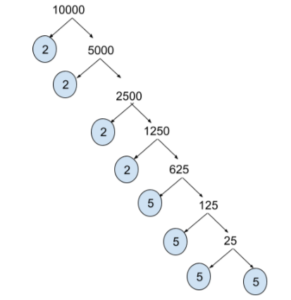
Hence, the smallest 5-digit number is 10000, and its prime factorisation using a tree diagram is 2×2×2×2×5×5×5×5.