Profile
Settings
Refer your friends
Sign out
H1: What is the value of sin and cos infinity? – Mathematics
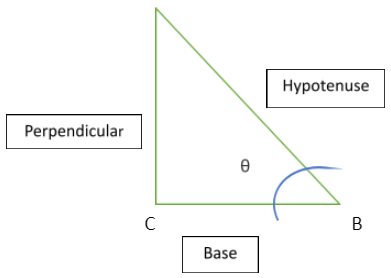
Answer: The trigonometric ratios refer to the ratios of length of the sides of a right-angled triangle to its respective angle. These trigonometric ratios are named as follows: sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosec and sec. Let us consider a right-angled triangle to understand these ratios.
Therefore
Sinθ= Perpendicular/Hypotenuse
Cosθ= Base/Hypotenuse
Tanθ= Perpendicular/Base
Secθ= Hypotenuse/Base
Cosecθ= Hypotenuse/Perpendicular
Cotθ= Base/Perpendicular
Hence for different angles i.e at 0, 30, 45, 60, 90 and infinity, the value of these ratios is different.
The following table shows the values of these ratios at different angles.
Angle | 0° | 30° | 45° | 60° | 90° |
Sin | 0 | 1/2 | 1/√2 | 3/2 | 1 |
Cos | 1 | 3/2 | 1/√2 | 1/2 | 0 |
Tan | 0 | 1/3 | 1 | 3 | Not Defined |
Hence, to find the value of sin and cos infinity, we have to follow the following steps:
It is known to us that,
(-1) ≤ sin x, cos x ≤ (+1) for x ε (- α, +α)
i.e., sin x and cos x values generally lie in between – 1 to 1.
Likewise, ∞ is not defined along these lines, sin (∞) and cos (∞) can’t have exact values.
Also, sin x and cos x are periodic functions with an oscillation of 2π.
Therefore, it can be said that the values of sin and cos infinity range between -1 to 1 and no exactly defined values are found.
