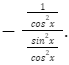What is the Derivative of Cosec x

How do you find the derivative of cot x?

The cot or cotangent function is the reciprocal of the tangent function. Mathematically, it can be represented as cot x = 1/tan x. Now, we know that tan x = sin x/cos x, so we can write cot x = cos x/sin x. 

To find the derivative if cot x, we are using three different methods.

• Derivative using Chain Rule

Since cot x = 1/tan x, we write

Now we know that tan x = sin x/cos x and sec x = 1/cos x. So, the derivative turns out to be

This can be simplified as -1/sin²x = -cosec²x. 

So,  (d/dx)cot x = -cosec²x

• Derivative using Quotient Rule

We can write cot x = cos x/sin x

So, (d/dx)cot x = (d/dx)(cos x/sin x)

This is an u/v form. According to quotient rule, if u and v are functions of x, then 

(d/dx)(u/v) = (u’v-v’u)/v²

Here, u = cos x and v = sin x. So, u’ = -sin x and v’ = cos x

So,

Since sin² x + cos² x = 1, we write the above expression as -1/sin² x = -cosec² x

So, (d/dx)cot x = -cosec²x

• Derivative Using First Principle

In this method, we use the basic definition of a derivative. For a function f(x), its derivative is written as 

So, considering f(x) = cot x, we get

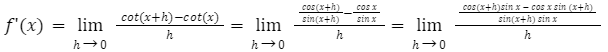
We know the addition subtraction formula in trigonometry, which states 

sin (A-B) = sin A cos B – cos A sin B.  Applying this formula in the above expression, we get

We can write this, since sin (-x) = -sin x

Using limits, we know 

So, we write 

So, (d/dx)cot x = -cosec²x

As we can see from these methods, the derivative of cot x is -cosec²x.