State BPT Theorem and Prove it

State BPT theorem and prove it

It was Thales, a famous Greek mathematician who introduced the BPT (Basic Proportionality Theorem) and is also known as Thales Theorem. 

Statement:

According to the BPT (Basic Proportionality Theorem), when a line is drawn parallel to one of the three sides of a triangle in such a way that it intersects the other two sides in distinct points, then the other two sides of the same triangle are divided into the same ratio. 

Proof:

Given:

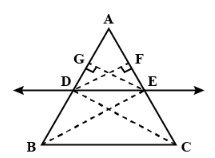
In ∆ABC, DE || BC and AB and AC are intersected by DE at points D and E respectively.

To prove:

AD / DB = AE / EC

Construction:

Join BE and CD.

Draw:

EG⊥AB and DF⊥AC

Proof:

It is known that

ar(ΔADE) = 1 / 2 × AD × EG   

ar(ΔDBE) = 1 / 2 × DB × EG   

Therefore, the ratio of these two can be computed as

ar(ΔADE) / ar(ΔDBE) = AD / DB   . . . . . . . . . . . . . . (1)

Similarly,

ar(ΔADE) = ar(ΔADE) = 1 / 2 × AE × DF    

ar(ΔECD) = 1 / 2 × EC × DF   

Therefore, the ratio of these two can be computed as

ar(ΔADE) / ar(ΔECD) = AE / EC   . . . . . . . . . . . .. . . (2)

Now, 

ΔDBE and ΔECD are the same base DE and also between the same parallels i.e. DE and BC, we can get 

ar(ΔDBE) = ar(ΔECD)   . . . . . . . . . . . (3)

From three equations 1, 2, 3 it can be concluded that

AD / DB = AE / EC  

Hence, the Basic Proportionality Theorem is proved.