Let n denote the set of all natural numbers and r be the relation on n times n defined by a b relation c d if ad times b plus c bc times a d then r is?

Answer: Let R be defined on N×N as

(a,b)R(c,d) ⇔ ad(b+c)

= bc(a+d). …(1) 

Reflexivity:
We can write ab(b+a) = ba(a+b) for all a,b ∈ N
Since natural numbers obey the commutative principle, their total and product are equal.
Hence, by def (1), we can write
(a,b) R (a,b) for all (a,b) ∈ N × N
Hence, R is reflexive.

Symmmetry:
Let⁡(a,b)R(c,d)

⇒ ad(b+c) = bc(a+d)

⇒da(c+b) = cb(d+a)

Since natural numbers obey the commutative principle, their total and product are equal.
or cb⁡(d+a) = da(c+b)

⇒ (c,d)R(a,b) 

Hence, R is symmetric

Transitivity:
Let (a,b),(c,d),(e,f)∈NN
Let (a,b)R(c,d) and (c,d)R(e,f)
ad(b+c) = bc(a+d) and cf(d+e) = de(c+f)

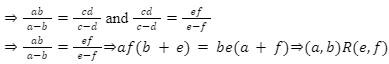
Hence, R is transitive

∴R is Equivalence Relation.