ABCD is a Trapezium in which AB Parallel DC and its Diagonals Intersect each other at Point O Show that AO/BO = CO/DO

Answer: Basic proportionality theorem states that – “If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other sides are divided proportionally”

Given: Trapezium ABCD and AB II DC

To Prove: AO/BO = CO/DO

Construction: Line MN running parallel to AB and DC through the intersection point O.

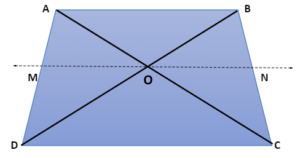
Proof: In triangle ABC,

ON II AB (by construction)

Now, according to basic proportionality theorem, 

BN/CN = AO/CO (Equation 1)

And In triangle BCD,

ON / CD (by construction)

Again, according to the basic proportionality theorem,

BN/CN = OB/OD (Equation 2)

Hence, from equations (1) and (2),

OA/OC = OB/OD

This implies, OA/OB = OC/OD

Hence Proved.