In the Logical Reasoning Section of the exam’s syllabus, questions regarding sequence arrangements are common. These are the most prevalent examinations, and you may find them in various entrance exams that include an aptitude test, such as the CAT and SBI PO. This emphasises the necessity of comprehending these types of issues. Arrangement questions might have different types, such as linear, circular or matrix arrangement problems. One particular problem on sequence arrangement encompasses roughly 4-5 sub-questions to assess an aspirant’s aptitude.
The Logical Reasoning (LR) section in the CAT focuses on the linear arrangement. Generally, it deals with successively aligning the items with the help of the information provided about their places in the questions themselves. In many circumstances, we must establish the exact placement of each item or the relative position of one thing concerning the others.
Linear Arrangement
Compared to other problems, logical reasoning questions on linear arrangements are generally easier. But students facing this section for the first time may struggle to understand the circumstances and usually become confused by the various constraints and statements presented in the logical reasoning set. It will be easier to master linear arrangement logical reasoning challenges if you prepare in a disciplined and step-by-step manner.
Types of Linear Arrangements
Linear arrangement problems can be broadly classified into two groups based on the pattern in which the arrangement of objects is done:
- Arrangement with only one row
- Arrangements with multiple rows
Although there is no major difference in method between these two sorts of linear arrangement in terms of strategy, the conditions for an arrangement with multiple row issues may be a bit more complicated.
Steps involved in solving linear arrangement questions
Unlike the concepts of mathematics, logical reasoning questions do not follow any particular pattern. As a result, the procedures for solving each linear arrangement issue may vary from question to question.
Given below is a list of the processes we normally undertake to arrange the data and arrive at a solution to most of these problems:
Pictorial representation
After reading the question, prepare a graphical linear sequence based on the number of items supplied in the reasoning set.
For example, imagine the question asks us to arrange five persons in a row in the order of their heights, that is, from the tallest to the shortest: Ram, Shyam, Arun, Anil, and Ravi. It’s also stated that none of them is of the same height. Then we may use the following visual representation of their standing stance as a guide:
_T__ ___ ___ ___ _S__
T- tallest
S- shortest
Symbolic representation
Consider the following constraint: the condition states that Ram is taller than Arun but shorter than Ravi, then Ravi>Ram>Arun can be used to represent the condition.
Another possibility is that only one individual is shorter than Shyam and taller than Anil. Syam_Anil is one approach to depict this circumstance symbolically.
There are endless ways or methods to represent symbols in this manner. Unfortunately, there are currently no commonly adopted standards of practice. Therefore, a student must develop a symbolic representation that they feel comfortable with.
The only suggestion we would like to provide is that your symbolic representation must be tidy, distinct and legible. So tidy, if you need to return to that representation, distinct, so you don’t mix up one sign with the others and legible, to not fail to understand them in the nervousness of solving the question.
Combining the conditions
Following the representation of the requirements, the constraint should be optimised to fulfil all of the conditions.
This is the most important phase, as it is here that the student’s capacity to reason and arrange material is shown. This problem may be solved with sufficient practice, the appropriate attitude, and sheer determination.
Matrix Arrangement
Except for a few more dimensions, complex arrangement issues are similar to linear arrangement problems. The following example of a question will help you better understand:
V, W, X, Y and Z are the five settlements. Two of them have a post office, three have schools, and three are road accessible. Two have populations of more than 5000 people each, two have populations of 2000 to 5000 people each, and one has a population of fewer than 2000 people. Two of these settlements have electricity and other amenities like schools and road access. A school exists in one village with fewer than 2000 people, but it lacks a post office and is not accessible by road, whereas each community with a population of more than 5000 people has a school. Only one of the two settlements, with a population of 2000 to 5000 people, has a post office and is accessible by road. V is reachable by car. W has a population of over 5000 people, Y has a school that is reachable by road but lacks a post office, and Z has a school that is not reachable by road.
Unlike linear arrangement issues, which offer easy information, you can see from the above example that it has three distinct features instead of just one. These added characteristics complicate the problems rather than solve them. The solution to the above problem can be attained using the Matrix method.
A table is drawn in this manner, with the first column designated for the objects or individuals whose qualities are specified in the problem. The remaining columns are utilised in listing the object’s numerous characteristics. Below is an example of the table.
A-V, B-W, C-X, D-Y, E-Z
The next step is to begin reading, putting up direct information linked with the item in the problem by using ‘+’ for yes and * for no. But, first, let’s get started with the data mentioned above.
- It has been stated that V is reachable by road.
- W has a population of above 5000 people.
- Although Y has a school and is accessible by road, it lacks a post office.
- Although Z has a school, it is not easily accessible by road.
- Place + and * signs in all relevant spots, as shown.
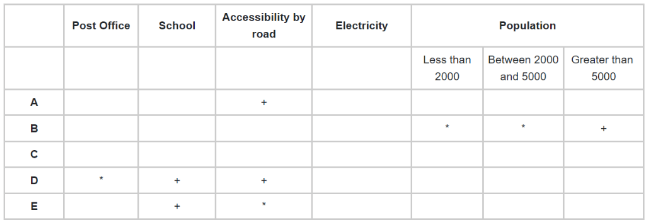
A-V, B-W, C-X, D-Y, E-Z
It has been stated that any village with a population greater than 5000 has a school, implying that W has a school. This point also implies that there are three schools, one of which we just established in W and the other two in Y and Z, implying that either Y or Z has a population greater than 5000. We may utilise the above data to determine which one has the population. One village with a population of fewer than 2000 has a school but no post office and is not accessible by road. Now, because Y is accessible by road, it can’t be the one with less than 2000 residents. Hence, Z is the one with fewer than 2000 residents. Also, there are no schools in V and W. Let’s now include this knowledge in our next matrix.

A-V, B-W, C-X, D-Y, E-Z
As it is evident, we’ve almost completed half of the matrix, and we can see that villages V and W both have populations of 2000 to 5000 people. However, only one of them has a post office and road access. Therefore, V must have a post office since it is accessible by road. Also, three villages have road access; we’ve identified two of them, leaving one, which should be WB because only one settlement with a population of 2000 to 5000 people has a post office and is accessible by road. So X can’t be the one, implying that Y does as well. Furthermore, two of these communities have electricity and certain other amenities such as schools and road connections, and W and Y are the only viable possibilities that meet these requirements. As a result, the subsequent matrix is:
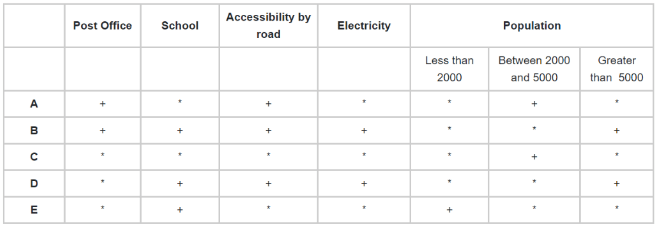
A-V, B-W, C-X, D-Y, E-Z
Once the constraints are completed and the matrix is drafted, you will be provided with a few sub-questions. For example, which community has a school and a post office, or which village lacks any of the amenities provided to the other villages to answer.
Conclusion
Data interpretation and logical reasoning are difficult sections of the exams, with several arrangements such as linear arrangement, matrix arrangement, circular arrangement, complex arrangement, etc. It requires immense practice and devotion.
Students are advised to follow these guidelines strictly:
- Practice regularly.
- Familiarise yourself with different kinds of sets.
- Understand your strengths.
- Learn to pick sets well.
- Practice again.
- Look at how toppers/guides solve it.
- Be methodical.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






