What is a vector?

A vector is a physical quantity with a magnitude and a direction associated with it. Vectors can have different notations like Matrix notation, Cartesian notation, and Polar notation. There are many cases where we use the benefit of symmetry of a given structure, for example, spherical symmetry or cylindrical symmetry. Now, let’s talk about different types of vectors:

1. Fixed vectors– These vectors have their initial and final points fixed.
2. Parallel vectors– If two vectors are parallel, we call them parallel vectors. Their cross-product is zero.
3. Position Vector– A vector denoting the position of a point concerning the origin is called a position vector.
4. Co–initial vectors– When two vectors have the same initial point or point of origin, they are called co-initial vectors.
5. Like vectors– If two vectors are in the same direction, they are called vectors.
6. Unlike vectors– If two vectors are in opposite directions, they are called unlike vectors.
7. Coplanar vectors– If two or more vectors lie in the same plane, they are called coplanar vectors.
8. Collinear vector- If two vectors are linear (parallel or antiparallel), they are called collinear vectors.

Properties of vectors

• If A, B, C are three vectors and follow the triangle law of addition

Then we can write

                              A=B+C=C+B

That means vector additions are commutative.

• We can shift a vector anywhere in the plane, keeping its direction fixed. That is, we can shift it parallelly.

As a sum of two vectors- The notation of a vector is given by an arrow. The tail of this arrow represents the initial point, and the tip of the arrow represents the final point of the vector.

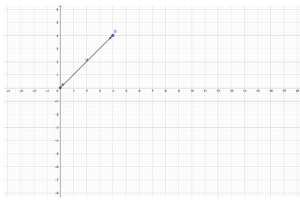
In the above diagram, we have a vector u which is shown.

In order to write a vector, we need base vectors which are unit vectors and called basis.

For two dimensions, we need two bases, along x it is I, and along Y it is j.

For example, in the given figure, we can write 

                                      u = 4i +4j          

1. Zero vector- It is a special case in which we assume a point as a vector having zero magnitudes, but the direction would be arbitrary as per convenience. This is the simplest form of vector.
2. Matrix notation- In this, we denote a vector in the form of a matrix. We know that a linear set of equations can be written in the form of a matrix, and equation 1 looks like a linear equation. In other words, this is a pseudo linear equation.

          We can write,

           u=4 4 0 where 0 represents no component in the z-direction.

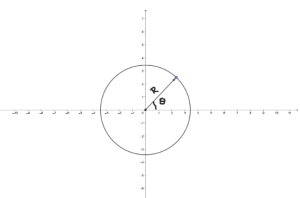
1. Polar notations- We can write a vector as a set of two or three parameters. The condition is that the surface on which the vector lies must be symmetric. It is used for non-linear or curved distances.

• The radial distance 
• Angle from the positive x-axis in a counter-clockwise direction

                 In the given figure, the vector R can be written as 

                                      R = (R, θ)

Product of two vectors

1. Dot product– This is a scalar product, which means the quantity we get after the product would be a scalar. This is represented by,

                                    A.B=AB cosθ 

1. Cross product– This is a vector product which means that after the multiplication, we get a vector quantity. This is represented by,

                          AB=ABsin   n                               

Where n is a unit vector perpendicular to the plane of A and B

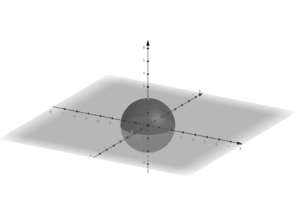
Similarly, for three dimensions, we have

                        u=xi+yj+zk   (in Cartesian form) 

This vector represents any point on the surface of the sphere.

Having magnitude, 

x2+y2+z2=u2

                  u=(r,θ, ϕ)          (in polar system)

Where,

 theta is the angle made by the projection of the R vector on the x-y plane with the positive x-axis, and r is the radial distance.

 ϕ is the angle made by the vector from the z-axis.

Conclusion

Vectors remind us of the importance of direction. If we are applying a force on any object, we have to be clear about the direction of using that force. Although we can move a vector freely through space, some vectors cannot be movable like fixed vectors.

Since there are a lot of mathematical tools available for vectors and matrices, we have the advantage of having this branch in physics. 

Vectors in two dimensions have two components and in three dimensions have three components. We can resolve every vector in the direction of their basis. In two dimensions, we have two bases perpendicular to each other, but it is not necessary that the basis must be perpendicular. They may or may not be perpendicular.