Profile
Settings
Refer your friends
Sign out
Moment of inertia is one of the fundamental concepts of physics. It was discovered by Galilio Galilei, who said that moment of inertia is a property of a body by its virtue that helps the body resist a change in its motion when an external force is applied to it.
The parallel axis theorem is used in order to calculate the moment of inertia of a body or the second moment of the area of a body. It is applicable to both two dimensional and three-dimensional bodies.
Parallel Axis Theorem Definition
According to the parallel axis theorem, the moment of inertia of a body about any axis is equal to the moment of inertia about the parallel axis through the centre of mass summed up with the product of the mass of the body and the square of the perpendicular distances between the two parallel axes.
This theorem is also known as Hygens-Steiner’s theorem. It was named after Christiaan Hygens and Jakob Steiner.
Formula of Parallel Axis theorem:
The formula of the parallel axis theorem is as follows:
Derivation of Parallel Axis Theorem
For the derivation of the parallel axis theorem, we need to prove that the moment of inertia of a body is the sum of the moment of inertia of that body about its centre and the product of mass and square of the distance between two axes.
Let us assume that Ic is the moment of inertia of the body shown above along an axis that passes through the centre of the body. I is the moment of inertia of this same body about the axis that lies at a distance of h from the centre which is A’B’.
Now, if r is the distance from the centre of gravity of this body, we will consider that mass m is present at this point r.
The distance from A’B’ then becomes h+r.
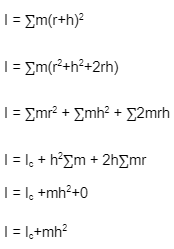
This is the final formula for the parallel axis theorem.
The parallel axis theorem can be applied on a rod to find its moment of inertia when one of the axes passes through the centre of the rod and the other, lets say, passes through one end of the rod.
The formula for the moment of inertia of a rod is given as ML²/12 if we are applying the parallel axis theorem. Lets see how:
The moment of inertia of a rod: I = ML²/3
The distance between the centre and one end of the rod of length: L= L/2
Then, according to the parallel axis theorem :
Example of Parallel Axis Theorem:
Suppose the moment of inertia of a box is 50 kg.m2 along an axis passing through its centre with the mass of the body being 30 kg, and another axis parallel to the present axis is present at a distance of 50 cm. What will be the moment of inertia along that axis?
Solution:
I=Ic+Mh²
I=50+(30*0.5²)
I=57.5 kg.m²
Conclusion
The parallel axis theorem was discovered to find the moment of inertia of an object in which the axis passed at a distance from the central axis. This makes it easy to be calculated especially for bodies that have an irregular shape. The parallel axis theorem can also be applied to 2D and 3D objects.
Though it is not applicable to a 3D object as a whole, it can be applied to it by dividing the object into smaller segments or laminas. Each lamina is then separately solved by applying a parallel axis theorem to it. It can only be applied to rigid bodies. There also exists an inertia matrix that differs each time one changes his/her point of reference.
